Question

1．已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=|x-1|+|x-2|-3，若对任意实数x，恒有f（x-a）≤f（x），则非零实数a的取值范围为[6，+∞）．

Answer 1

分析 可以采用数形结合的方法解决，“对任意的x∈R，恒有f（x-a）≤f（x）”也就相当于在实数集R上，f（x-a）的图象恒在f（x）的图象下方，画出f（x）和f（x-a）的图象，据此列出关于a的不等式解出来即可．

解答 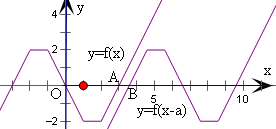解：函数f（x）是定义在R上的奇函数，
当x≥0时，f（x）=|x-1|+|x-2|-3，
当x＜0时，-x＞0，可得f（-x）=|-x-1|+|-x-2|-3=-f（x），
即有f（x）=3-|x+1|-|x+2|（x＜0），
作出y=f（x）的图象，y=f（x-a）的图象可由f（x）的图象
平移可得．
由题意可得在实数集R上，f（x-a）的图象恒在f（x）的图象下，
所以只需y=f（x）与x轴最右边的交点A（3，0）
在y=f（x-a）与x轴最左边交点B（-3+a，0）的左边或重合．
因此应该有3≤-3+a，即a≥6．
故答案为：[6，+∞）．

点评 这道题是将不等式恒成立问题转化为函数的最值问题，因为问题相对复杂，因此借助于数形结合，使得问题变得简单明了，注意此法适合于选择、填空题．