
分析 由已知求出$\overrightarrow{a}•\overrightarrow{b}$.
(1)把要求得数量积展开,代入${\overrightarrow{a}}^{2}、{\overrightarrow{b}}^{2}、\overrightarrow{a}•\overrightarrow{b}$得答案;
(2)求出$|3\overrightarrow{a}-4\overrightarrow{b}{|}^{2}$,开方得答案.
解答 解:由$\overrightarrow a$,$\overrightarrow b$的夹角为120°,且|$\overrightarrow a$|=4,|$\overrightarrow b$|=2,得
$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos 120°=4×2×(-$\frac{1}{2}$)=-4.
(1)($\overrightarrow a$-2$\overrightarrow b$)•($\overrightarrow a$+$\overrightarrow b$)=${\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+\overrightarrow{a}•\overrightarrow{b}-2{\overrightarrow{b}}^{2}$=42-2×(-4)+(-4)-2×22=12;
(2)∵$|3\overrightarrow{a}-4\overrightarrow{b}{|}^{2}=9{\overrightarrow{a}}^{2}-24\overrightarrow{a}•\overrightarrow{b}+16{\overrightarrow{b}}^{2}$=9×42-24×(-4)+16×22=16×19,
∴|3$\overrightarrow a$-4$\overrightarrow b$|=4$\sqrt{19}$.
点评 本题考查平面向量的数量积运算,考查向量模的求法,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
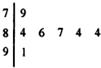 在某校举办的“激扬青春,勇担责任”演讲比赛中,有七位评委选手打分,若选手甲所得分数用茎叶图表示如图,则选手甲所得分数的中位数为( )
在某校举办的“激扬青春,勇担责任”演讲比赛中,有七位评委选手打分,若选手甲所得分数用茎叶图表示如图,则选手甲所得分数的中位数为( )| A. | 87 | B. | 86 | C. | 85 | D. | 84 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [0,4] | C. | {1,2,3,4} | D. | {0,1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
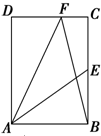
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q是假命题 | B. | p∨(¬q)是假命题 | C. | p∧q是真命题 | D. | p∧(¬q)是真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com