
| A. | ?x∈R,lgx=0 | B. | ?x∈R,x3>0 | C. | ?x∈R,tanx=1 | D. | ?x∈R,2x>0 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
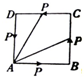 如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )
如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$-2 | D. | 3$\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
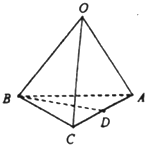 如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )
如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )| A. | -$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ | B. | $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
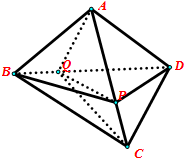 如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )
如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )| A. | 22 | B. | 34 | C. | 32 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x±9y=0 | B. | 9x±4y=0 | C. | 3x±2y=0 | D. | 2x±3y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com