
|
| m |
| 2 |
| m2 |
| 4 |
|
| m |
| 2 |
| 9-1 |
| 2 |
| 2 |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
| ln(-x) |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
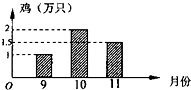 为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查.表格表示每个月所调查的养鸡场的个数,如图表示三个月中各养鸡场注射了疫苗的鸡的数量的平均数.根据图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为
为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查.表格表示每个月所调查的养鸡场的个数,如图表示三个月中各养鸡场注射了疫苗的鸡的数量的平均数.根据图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为| 月份 | 养鸡场(个数) |
| 9 | 20 |
| 10 | 50 |
| 11 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(-1,6) |
| B、[-1,6] |
| C、(-∞,-1)∪(6,+∞) |
| D、(-∞,-1]∪[6,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com