
椭圆 与双曲线
与双曲线 有公共的焦点,过椭圆
有公共的焦点,过椭圆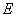 的右焦点作任意直线
的右焦点作任意直线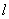 ,设直线
,设直线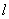 交抛物线
交抛物线 于
于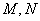 两点,且
两点,且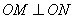
(1)求椭圆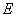 的方程;
的方程;
(2)设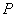 是椭圆
是椭圆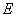 上第一象限内的点,点
上第一象限内的点,点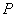 关于原点
关于原点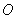 的对称点为
的对称点为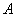 ,关于
,关于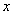 轴的对称点为
轴的对称点为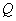 ,线段
,线段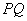 与x轴相交于点
与x轴相交于点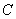 ,点
,点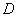 为
为 的中点,若直线
的中点,若直线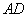 与椭圆
与椭圆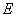 的另一个交点为
的另一个交点为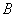 ,试判断直线
,试判断直线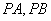 是否相互垂直?并证明你的结论。
是否相互垂直?并证明你的结论。
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
2014年亚冠联赛中国共有四支足球队参赛,分别为广州恒大、贵州人和、山东鲁能和背景国安,为了打出中国足球的精神面貌,足协项派五名官员给这四支球队做动员工作,每支球队至少派一名官员,且甲、乙官员不能到同一支球队,则不同的安排方法的种数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com