
分析 (1)求出圆心到直线的距离,|AB|,即可求△ABC的面积;
(2)直线l:x+y+m=0,圆C:(x-2)2+(y-1)2=9联立,利用韦达定理,结合k1•k2=-2.斜率公式,即可求实数m的值.
解答 解:(1)若m=-2,直线l:x+y-2=0,∴圆心到直线的距离d=$\frac{|2+1-2|}{\sqrt{2}}$=$\frac{1}{\sqrt{2}}$,
∴|AB|=2$\sqrt{9-\frac{1}{2}}$=$\sqrt{34}$,
∴△ABC的面积S=$\frac{1}{2}×\sqrt{34}×\frac{1}{\sqrt{2}}$=$\frac{\sqrt{17}}{2}$;
(2)设A(x1,y1),B(x2,y2)
直线l:x+y+m=0,圆C:(x-2)2+(y-1)2=9联立可得2x2+(2m-2)x+m2+2m-4=0.
∴x1+x2=1-m,x1x2=$\frac{1}{2}$(m2+2m-4)
k1•k2=$\frac{{y}_{1}-1}{{x}_{1}-2}$•$\frac{{y}_{2}-1}{{x}_{2}-2}$=$\frac{{x}_{1}{x}_{2}+(m+1)({x}_{1}+{x}_{2})+(m+1)^{2}}{{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+4}$=-2,
∴3x1x2+(m-3)(x1+x2)+(m+1)2+8=0
∴3•$\frac{1}{2}$(m2+2m-4)+(m-3)(1-m)+(m+1)2+8=0,
∴m2+4m-2=0,
∴m=-2±$\sqrt{6}$
点评 本题考查三角形面积的计算,考查直线与圆的位置关系,考查韦达定理的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
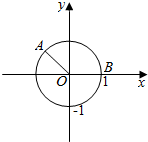 已知点A,B在单位圆上,A(-$\frac{3}{5}$,$\frac{4}{5}$),B(1,0),∠BOA=a,如图所示
已知点A,B在单位圆上,A(-$\frac{3}{5}$,$\frac{4}{5}$),B(1,0),∠BOA=a,如图所示查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {1,2} | C. | {1,3} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,-4,6) | B. | (-6,-6,-5) | C. | (10,0,7) | D. | (10,-6,19) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com