
| A. | $\frac{4}{3}$ | B. | 4 | C. | 6 | D. | 12 |
分析 过B向准线做垂线垂足为D,过A点向准线做垂线垂足为E,准线与x轴交点为H,根据抛物线性质可知|BD|=|BF|,根据|BC|=2|BF|,判断∠C=30°,进而可知,∠EAC=60°,根据|AF|=|AE|进而判断三角形AEF为正三角形.进而可知∠FEC=30°,推断出|AF|=|AE|=EF|,根据|EF|=2|HF|求得|EF|答案可得.
解答 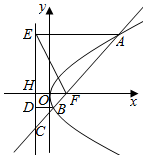 解:y2=4x的焦点F为(1,0),准线为x=-1,
解:y2=4x的焦点F为(1,0),准线为x=-1,
过B向准线作垂线垂足为D,
过A点向准线做垂线垂足为E,准线与x轴交点为H,
根据抛物线性质可知|BD|=|BF
∵|BC|=2|BF|,∴|BC|=2|BD|,
∴∠C=30°,∠EAC=60°
又∵|AF|=|AE|,
∴∠FEA=60°
∴|AF|=|AE|=EF|,
∵|EF|=2|HF|=4,即有|AF|=4.
故选:B.
点评 本题主要考查了抛物线的实际应用,注意运用抛物线的定义,考查直角三角形的性质以及运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{3},1)$ | B. | $(-∞,\frac{1}{3})∪(1,+∞)$ | C. | $(-\frac{1}{3},\frac{1}{3})$ | D. | $(-∞,-\frac{1}{3})∪(\frac{1}{3},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
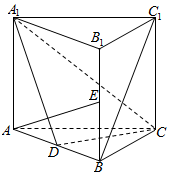 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com