
分析 (1)通过等差数列的概念直接计算即可;
(2)通过(1)及a2=7得an=11-2n,通过T2=a2+a3,b3=a3可得bn=$(\frac{1}{3})^{n-3}$,利用An-$\frac{1}{3}$An、错位相减法计算即得结论.
解答 解:(1)设等差数列{an}公差为d,由S6+8a7=0得a1=-$\frac{9}{2}d$,
则$\frac{{S}_{7}}{{a}_{6}}$=$\frac{7{a}_{1}+21d}{{a}_{1}+5d}$=$\frac{7(-\frac{d}{2})+21d}{-\frac{d}{2}+5d}$=-21;
(2)由a2=7得a1+d=7,则有$\left\{\begin{array}{l}{{a}_{1}=-\frac{9}{2}d}\\{{a}_{1}+d=7}\end{array}\right.$,
故a1=9,d=-2,∴an=11-2n,
设等比数列{bn}公比为q,由T2=a2+a3,b3=a3,
得:$\left\{\begin{array}{l}{{b}_{1}+{b}_{1}q=12}\\{{b}_{1}{q}^{2}=1}\end{array}\right.$,解得q=$\frac{1}{3}$或q=-$\frac{1}{4}$,
又b2>0,则q=-$\frac{1}{4}$(舍去),
∴q=$\frac{1}{3}$,b1=9,
∴bn=9×$(\frac{1}{3})^{n-1}$=$(\frac{1}{3})^{n-3}$,
则An=9×$(\frac{1}{3})^{-2}$+7×$(\frac{1}{3})^{-1}$+5×$(\frac{1}{3})^{0}$+…+(11-2n)×$(\frac{1}{3})^{n-3}$,
$\frac{1}{3}$An=9×$(\frac{1}{3})^{-1}$+7×$(\frac{1}{3})^{0}$+…+(13-2n)×$(\frac{1}{3})^{n-3}$+(11-2n)×$(\frac{1}{3})^{n-2}$,
两式相减得:$\frac{2}{3}$An=9×$(\frac{1}{3})^{-2}$-2[$(\frac{1}{3})^{-1}$+$(\frac{1}{3})^{0}$+…+$(\frac{1}{3})^{n-3}$]-(11-2n)×$(\frac{1}{3})^{n-2}$,
化简得:An=108-$\frac{n-4}{{3}^{n-3}}$.
点评 本题考查求数列的通项及求和,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
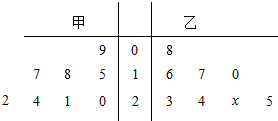 如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.
如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
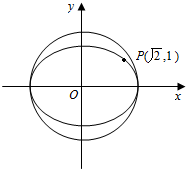 如图,椭圆:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率与双曲线x2-y2=4的离心率互为倒数,且内切于圆x2+y2=4.
如图,椭圆:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率与双曲线x2-y2=4的离心率互为倒数,且内切于圆x2+y2=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | B. | 若ac2>bc2,则a>b | C. | 若a>b,则ac>bc | D. | 若a>b,则(${\frac{1}{2}}$)a>(${\frac{1}{2}}$)b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com