练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．若复数z满足z（2-i）=i，则|z|=（　　）
    A．$\frac{1}{5}$B．$\frac{{\sqrt{5}}}{5}$C．$\frac{{\sqrt{5}}}{3}$D．$\sqrt{5}$

    分析 利用复数的运算法则、模的计算公式即可得出．

    解答 解：z（2-i）=i，∴z（2-i）（2+i）=i（2+i），∴5z=2i-1．即z=$-\frac{1}{5}$+$\frac{2}{5}$i．
    则|z|=$\sqrt{（-\frac{1}{5}）^{2}+（\frac{2}{5}）^{2}}$=$\frac{\sqrt{5}}{5}$．
    故选：B．

    点评 本题考查了复数的运算法则、模的计算公式，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．角α的终边经过的一点P的坐标是（-$\sqrt{3}$，a），则“|a|=1”的充要条件是（　　）
    A．$sinα=\frac{1}{2}$B．$cosα=-\frac{{\sqrt{3}}}{2}$C．$tanα=-\frac{{\sqrt{3}}}{3}$D．$|PO|=\sqrt{3}+1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设f（x）=$\frac{{e}^{x}-1}{x}$-ax-b（a、b∈R，e为自然对数的底数）．
    （1）若曲线y=f（x）在点（1，f（1））处的切线方程为x+2y+4=0，求a、b的值；
    （2）当b=1时，若总存在负实数m，使得当x∈（m，0）时，f（x）＜0恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

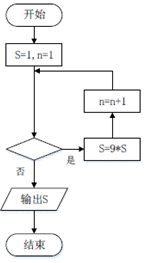    10．我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”：今有出门重九堤，堤有九木，木有九枝，枝有九巢，巢有九禽，禽有九雏，雏有九毛，毛有九色，问各几何？现在我们用右图所示的程序框图来解决这个问题，如果要使输出的结果为禽的数目，则在该框图中的判断框中应该填入的条件是（　　）
    A．S＞10000？B．S＜10000？C．n≥5D．n≤6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．如图1所示，在等腰梯形ABCD中，$BE⊥AD，BC=3，AD=15，BE=3\sqrt{3}$．把△ABE沿BE折起，使得$AC=6\sqrt{2}$，得到四棱锥A-BCDE．如图2所示．

    （1）求证：面ACE⊥面ABD；
    （2）求平面ABE与平面ACD所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知2a+2b=2c，则a+b-2c的最大值等于（　　）
    A．-2B．-1C．$\frac{1}{4}$D．-$\frac{1}{4}$

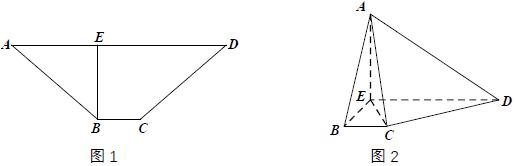
    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知F为抛物线C：x2=2py（p＞0）的焦点，过F的直线l与C交于A，B两点，M为AB中点，点M到x轴的距离为d，|AB|=2d+1．
    （1）求p的值；
    （2）过A，B分别作C的两条切线l1，l2，l1∩l2=N．请选择x，y轴中的一条，比较M，N到该轴的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

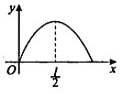    15．动点P从点A出发，按逆时针方向沿周长为1的平面图形运动一周，A，P两点间的距离y与动点P所走过的路程x的关系如图所示，那么动点P所走的图形可能是（　　）
    A．B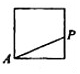．C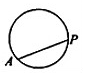．D．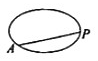

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知函数f（x）=$\left\{\begin{array}{l}{e^x}，x≤0\\{x^2}-2x+a+1，x＞0\end{array}$，若函数g（x）=f（x）-ax-1有4个零点，则实数a的取值范围为（0，1）．

    查看答案和解析>>

    同步练习册答案