
分析 (1)利用抛物线的定义,建立方程,即可得出结论;
(2)判断xM=xN,$|{y_M}|-|{y_N}|=|{{k^2}+\frac{1}{2}}|-|{-\frac{1}{2}}|={k^2}≥0$,即可得出结论.
解答 解:(1)设抛物线C的准线为m,如图,过A,B,M分别作直线m的垂线,垂足分别为A1,B1,M1.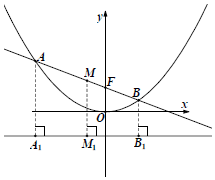
$|{AB}|=|{AF}|+|{BF}|=|{A{A_1}}|+|{B{B_1}}|=2|{M{M_1}}|=2({d+\frac{p}{2}})$,
所以$2({d+\frac{p}{2}})=2d+1$,所以p=1.
(2)由(1)得,抛物线$C:{x^2}=2y,F({0,\frac{1}{2}})$,
因为直线l不垂直于x轴,可设$l:y=kx+\frac{1}{2},A({{x_1},{y_1}}),B({{x_2},{y_2}}),M({{x_M},{y_M}}),N({{x_N},{y_N}})$.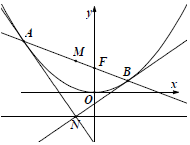
由$\left\{{\begin{array}{l}{{x^2}=2y}\\{y=kx+\frac{1}{2}}\end{array}}\right.$,消去y得,x2-2kx-1=0,
由韦达定理得,$\left\{{\begin{array}{l}{{x_1}+{x_2}=2k}\\{{x_1}{x_2}=-1}\end{array}}\right.$,
所以${x_M}=\frac{{{x_1}+{x_2}}}{2}=k,{y_M}={k^2}+\frac{1}{2}$.
抛物线C:x2=2y,即$y=\frac{1}{2}{x^2}$,故y'=x,
因此,切线l1的斜率为x1,切线l1的方程为y=x1(x-x1)+y1,
整理得${l_1}:y={x_1}x-\frac{1}{2}x_1^2$①,
同理可得${l_2}:y={x_2}x-\frac{1}{2}x_2^2$②,
联立①②并消去y,得$x=\frac{{{x_1}+{x_2}}}{2}=k$,
把$x=\frac{{{x_1}+{x_2}}}{2}$代入①,得$y=\frac{1}{2}{x_1}{x_2}=-\frac{1}{2}$,故$N({k,-\frac{1}{2}})$.
因为xM=xN,$|{y_M}|-|{y_N}|=|{{k^2}+\frac{1}{2}}|-|{-\frac{1}{2}}|={k^2}≥0$,
所以M,N到y轴的距离相等;M到x轴的距离不小于N到x轴的距离.
(注:只需比较M,N到x轴或y轴的距离中的一个即可)
点评 本题考查抛物线的定义,直线与抛物线位置关系的运用,考查韦达定理的运用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
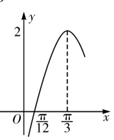 函数f(x)=Asin(ωx+θ)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,得到函数g(x)的图象,则g(x)在[0,$\frac{π}{6}$]上的取值范围为( )
函数f(x)=Asin(ωx+θ)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位,纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$后,得到函数g(x)的图象,则g(x)在[0,$\frac{π}{6}$]上的取值范围为( )| A. | [-$\sqrt{2}$,2] | B. | (-1,$\sqrt{2}$] | C. | [0,2] | D. | [-2,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$-1 | B. | $\sqrt{5}$+1 | C. | 2$\sqrt{5}$+2 | D. | 2$\sqrt{5}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com