
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可;也可结合正弦函数的图象和性质可得|x1-x2|min=$\frac{π}{2}$-φ=$\frac{π}{3}$,从而解得φ的值.
解答 解:将函数y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数g(x)=sin2x的图象,故f(x)=sin(2x-2φ),
当x1,x2满足时|f(x1)-g(x2)|=2 时,${|{{x_1}-{x_2}}|_{min}}=\frac{π}{3}$,
由题意可得:有|x1-x2|min=$\frac{π}{2}$-φ=$\frac{π}{3}$,
结合范围0<φ<$\frac{π}{2}$,解得:φ=$\frac{π}{6}$,
故选:D.
点评 本题考查三角函数的图象平移,函数的最值以及函数的周期的应用,考查分析问题解决问题的能力,是好题,题目新颖,有一定难度.其中,判断有|x1-x2|min=$\frac{T}{2}$-φ=$\frac{π}{2}$-φ,是解题的关键,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{5}{3}$ | D. | -$\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $sinα=\frac{1}{2}$ | B. | $cosα=-\frac{{\sqrt{3}}}{2}$ | C. | $tanα=-\frac{{\sqrt{3}}}{3}$ | D. | $|PO|=\sqrt{3}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 档次 人群 | 0~ 500元 | 500~ 1000元 | 1000~ 1500元 | 1500~ 2000元 |
| A类 | 20 | 50 | 20 | 10 |
| B类 | 50 | 30 | 10 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
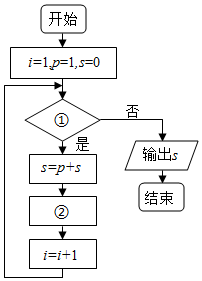 给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )
给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )| A. | i≤40?;p=p+i-1 | B. | i≤41?;p=p+i-1 | C. | i≤41?;p=p+i | D. | i≤40?;p=p+i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (2,2,3) | (3,2,3) | (3,3,3) | (1,2,2) | (2,3,2) | (2,3,3) | (2,2,2) | (2,3,3) | (2,1,1) | (2,2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com