
| 档次 人群 | 0~ 500元 | 500~ 1000元 | 1000~ 1500元 | 1500~ 2000元 |
| A类 | 20 | 50 | 20 | 10 |
| B类 | 50 | 30 | 10 | 10 |
分析 (Ⅰ)根据题意,设此人属于中低消费人群为事件M,分析可得A类样本共100人,属于中低消费的有20+50=70人,由古典概型公式计算可得答案;
(Ⅱ)设甲的消费档次不低于乙的消费档次为事件N,依次对乙的消费情况分4种情况讨论,求出每一种情况下的概率,由互斥事件的概率公式计算可得答案;
(Ⅲ)由频率分布表分析可得答案.
解答 解:(Ⅰ)设此人属于中低消费人群为事件M,
A类样本共100人,属于中低消费的有20+50=70人,
则 $P(M)=\frac{20+50}{100}$=0.7,
(Ⅱ)设甲的消费档次不低于乙的消费档次为事件N,
分4种情况讨论:
若乙的消费档次为0-500元,此时甲的消费档次不低于乙的消费档次的概率为P1=$\frac{5}{10}$×1,
若乙的消费档次为500-1000元,此时甲的消费档次不低于乙的消费档次的概率为P2=$\frac{3}{10}×\frac{8}{10}$,
若乙的消费档次为1000-1500元,此时甲的消费档次不低于乙的消费档次的概率为P3=$\frac{1}{10}×\frac{3}{10}$,
若乙的消费档次为1500-2000元,此时甲的消费档次不低于乙的消费档次的概率为P4=$\frac{1}{10}$×$\frac{1}{10}$,
则 $P(N)=\frac{5}{10}×1+\frac{3}{10}×\frac{8}{10}+\frac{1}{10}×\frac{3}{10}+\frac{1}{10}×\frac{1}{10}$=$\frac{50}{100}+\frac{24}{100}+\frac{3}{100}+\frac{1}{100}$=0.78,
(Ⅲ)由统计表分析可得B类分布较为分散,则B的方差比较大.
答:B
点评 本题考查古典概型的计算,涉及频率分布表的应用,关键是读懂频率分布表.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:解答题
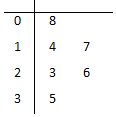 据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级.某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级.某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y-2=0 | B. | 2x-y-1=0 | C. | 2x+y-6=0 | D. | 2x+y-3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com