
分析 (1)化简f(x)的解析式,判断f(x)的单调性,根据单调性得出f(x)的最小值化简即可得出结论;
(2)分离参数得t≤$\frac{a+2b}{ab}$,把2a+b=2代入不等式,根据基本不等式的性质得出$\frac{a+2b}{ab}$的最小值,从而得出t的范围.
解答 解:(1)证明:令x+a=0得x=-a,令2x-b=0得x=$\frac{b}{2}$,
∵a>0,b>0,∴-a$<\frac{b}{2}$,
则f(x)=$\left\{\begin{array}{l}{-3x-a+b,x≤-a}\\{-x+a+b,-a<x<\frac{b}{2}}\\{3x+a-b,x≥\frac{b}{2}}\end{array}\right.$,
∴f(x)在(-∞,$\frac{b}{2}$]上单调递减,在($\frac{b}{2}$,+∞)上单调递增,
∴fmin(x)=f($\frac{b}{2}$)=a+$\frac{b}{2}$=1,2a+b=2;
(2)∵a+2b≥tab恒成立,∴t≤$\frac{a+2b}{ab}$恒成立,
∵2a+b=2,∴a+$\frac{1}{2}$b=1,
∴$\frac{a+2b}{ab}$=$\frac{1}{b}$+$\frac{2}{a}$=$\frac{a+\frac{1}{2}b}{b}$+$\frac{2a+b}{a}$=$\frac{5}{2}$+$\frac{a}{b}+\frac{b}{a}$≥$\frac{5}{2}+2$=$\frac{9}{2}$,(当且仅当a=b时取等号)
∴$\frac{a+2b}{ab}$的最小值为$\frac{9}{2}$,
∴t$≤\frac{9}{2}$.
点评 本题考查了函数单调性的判断与最值计算,基本不等式的应用,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{\sqrt{35}}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $sinα=\frac{1}{2}$ | B. | $cosα=-\frac{{\sqrt{3}}}{2}$ | C. | $tanα=-\frac{{\sqrt{3}}}{3}$ | D. | $|PO|=\sqrt{3}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 档次 人群 | 0~ 500元 | 500~ 1000元 | 1000~ 1500元 | 1500~ 2000元 |
| A类 | 20 | 50 | 20 | 10 |
| B类 | 50 | 30 | 10 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (2,2,3) | (3,2,3) | (3,3,3) | (1,2,2) | (2,3,2) | (2,3,3) | (2,2,2) | (2,3,3) | (2,1,1) | (2,2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
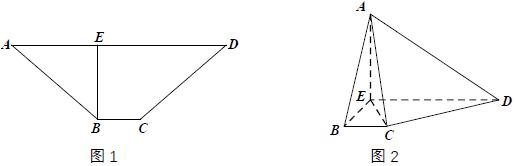
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com