
| A�� | ��=0 | B�� | $\overrightarrow{n}$=0 | C�� | $\overrightarrow{m}$��$\overrightarrow{n}$ | D�� | ��=0��$\overrightarrow{m}$��$\overrightarrow{n}$ |
���� ����$\overrightarrow{a}$��$\overrightarrow{b}$���ߣ����ж�$\overrightarrow{b}$�Ƿ�Ϊ$\overrightarrow{0}$��$\overrightarrow{b}=\overrightarrow{0}$ʱ������$\overrightarrow{a}��\overrightarrow{b}$���ߣ�����ʱ��õ���=0����$\overrightarrow{m}��\overrightarrow{n}$����$\overrightarrow{b}��\overrightarrow{0}$ʱ���������������жϳ�$\overrightarrow{n}$��$\overrightarrow{b}$���ߣ�$\overrightarrow{m}$��$\overrightarrow{b}$���ߣ��Ӷ���ɵó�$\overrightarrow{m}��\overrightarrow{n}$���������ó���=0����$\overrightarrow{m}��\overrightarrow{n}$��
��� �⣺��1����$\overrightarrow{n}=\overrightarrow{0}$����$\overrightarrow{b}=\overrightarrow{0}$������$\overrightarrow{a}$��$\overrightarrow{b}$���ߣ���ʱ$\overrightarrow{m}��\overrightarrow{n}$��
��2����$\overrightarrow{n}��\overrightarrow{0}$����=0����$\overrightarrow{b}=\overrightarrow{0}$������$\overrightarrow{a}$��$\overrightarrow{b}$���ߣ���ʱ��=0��
��3����$\overrightarrow{n}��\overrightarrow{0}$���ˡ�0����$\overrightarrow{b}��\overrightarrow{0}$��
��$\overrightarrow{b}=��\overrightarrow{n}$��$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{m}$��$\overrightarrow{a}$��$\overrightarrow{b}$���ߣ�
��$\overrightarrow{n}$��$\overrightarrow{b}$���ߣ�$\overrightarrow{m}$��$\overrightarrow{b}$���ߣ�
��$\overrightarrow{m}$��$\overrightarrow{n}$���ߣ���$\overrightarrow{m}��\overrightarrow{n}$��
�����ϵæ�=0����$\overrightarrow{m}$��$\overrightarrow{n}$��
��ѡ��D��
���� ���鹲�������ĸ��֪�����������κη����������ߣ�������$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{m}$��$\overrightarrow{a}��\overrightarrow{b}$����ʱ����õ�$\overrightarrow{m}$��$\overrightarrow{b}$��$\overrightarrow{a}$�����ߣ�������������һ��������������ʱ���������������ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
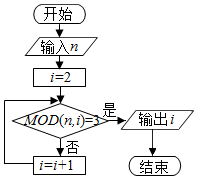 ��֪MOD������һ�����ຯ�������ʽΪMOD��n��m��������Ϊn����m������������MOD��7��3��=1����ͼ��һ���㷨�ij����ͼ���������nֵΪ15ʱ������Ľ��Ϊ��������
��֪MOD������һ�����ຯ�������ʽΪMOD��n��m��������Ϊn����m������������MOD��7��3��=1����ͼ��һ���㷨�ij����ͼ���������nֵΪ15ʱ������Ľ��Ϊ��������| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ�����ֲ���Ҫ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com