
 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,与x轴交于点C,与y轴交于点D,已知OA=$\sqrt{10}$,点B的坐标为(m,-2),tan∠AOC=$\frac{1}{3}$.
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,与x轴交于点C,与y轴交于点D,已知OA=$\sqrt{10}$,点B的坐标为(m,-2),tan∠AOC=$\frac{1}{3}$.分析 (1)过A作AE⊥x轴于E,tan∠AOE=$\frac{1}{3}$,可得OE=3AE,利用勾股定理得,可得AE=1,OE=3,A的坐标为(3,1),A点在双曲线上,可得反比例函数,B(m,-2)在双曲线上,可得B的坐标,可得一次函数的解析式;
(2)三角形S△AOB=S△AOD+S△BOD,利用坐标可求.
(3)过点C作CP⊥AB,交y轴于点P,C,D在直线AB上.此时△PDC与△CDO相似,可得P的坐标.
解答 解:(1)过A作AE⊥x轴于E,tan∠AOE=$\frac{1}{3}$,∴OE=3AE,
∵OA=$\sqrt{10}$,由勾股定理得:OE2+AE2=10,解得:AE=1,OE=3,∴A的坐标为(3,1),
∵A点在双曲线上y=$\frac{k}{x}$上,∴1=$\frac{k}{3}$,∴k=3,
∴双曲线的解析式y=$\frac{3}{x}$;
∵B(m,-2)在双曲y=$\frac{3}{x}$上,∴-2=$\frac{3}{m}$,解得:m=-$\frac{3}{2}$,∴B的坐标是(-$\frac{3}{2}$,-2),
代入一次函数的解析式得:$\left\{\begin{array}{l}{3a+b=1}\\{-\frac{3}{2}a+b=-2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-1}\end{array}\right.$
则一次函数的解析式为:y=$\frac{2}{3}$x-1;
(2)连接BO,∵一次函数的解析式为:y=$\frac{2}{3}$x-1;
∴D(0,-1),
∴三角形S△AOB=S△AOD+S△BOD=$\frac{1}{2}$×DO×3+$\frac{1}{2}$×DO×$\frac{3}{2}$=$\frac{9}{4}$.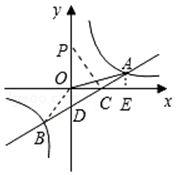
(3)过点C作CP⊥AB,交y轴于点P,
∵C,D两点在直线y=$\frac{2}{3}$x-1上,
∴C,D的坐标分别是:C(,0),D(0,-1).
即:OC=$\frac{3}{2}$,OD=1,∴DC=$\frac{\sqrt{13}}{2}$.
∵△PDC∽△CDO,∴$\frac{PD}{DC}=\frac{DC}{DO}$,∴PD=$\frac{D{C}^{2}}{DO}$,
又∵OP=DP-OD=$\frac{13}{4}$-1=$\frac{9}{4}$,
∴P点坐标为(0,$\frac{9}{4}$).
点评 本题考查了反比例函数、一次函数的解析式求法,三角形的面积求法和相似三角形的性质运用.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,1) | C. | [0,1) | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=|x|+1 | C. | y=-x2+1 | D. | $y=\frac{1}{x^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=5${\;}^{\frac{1}{2-x}}$ | B. | y=log2(3x+2) | C. | y=$\sqrt{1-{2}^{x}}$ | D. | y=($\frac{1}{3}$)1-x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com