
分析 依题意,可知α≠$\frac{3π}{2}$且β≠$\frac{3π}{2}$,由-1<7m-3≤1,-1<1-m≤1,可解得:$\frac{2}{7}$<m≤$\frac{4}{7}$①;进一步可分析出sinα>sin(2π-β)=-sinβ,即7m-3>m-1,解得:m>$\frac{1}{3}$②;从而可得答案.
解答 解:∵$α∈[\frac{π}{2},\frac{3π}{2}]$,$β∈[\frac{π}{2},\frac{3π}{2}]$,且α+β<2π,
∴α≠$\frac{3π}{2}$且β≠$\frac{3π}{2}$,
又sinα=7m-3,sinβ=1-m,
∴-1<7m-3≤1,-1<1-m≤1,
解得:$\frac{2}{7}$<m≤$\frac{4}{7}$①;
由α+β<2π得:α<2π-β,
又$β∈[\frac{π}{2},\frac{3π}{2}]$,故2π-β∈$[\frac{π}{2},\frac{3π}{2}]$,而$α∈[\frac{π}{2},\frac{3π}{2}]$,y=sinx在区间$[\frac{π}{2},\frac{3π}{2}]$上单调递减,
∴sinα>sin(2π-β)=-sinβ,即7m-3>m-1,解得:m>$\frac{1}{3}$②;
由①②得实数m的取值范围为:$(\frac{1}{3},\frac{4}{7}]$.
故答案为:$({\frac{1}{3},\frac{4}{7}}]$.
点评 本题考查三角函数的最值,分析得到sinα>sin(2π-β)是关键,也是难点,考查推理与运算能力,属于难题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1011001(2) | B. | 1110101(2) | C. | 1010101(2) | D. | 1101001(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
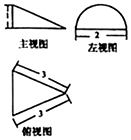
| A. | $\frac{{\sqrt{2}}}{3}π$ | B. | $\frac{π}{2}$ | C. | $\frac{{2\sqrt{2}}}{3}π$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
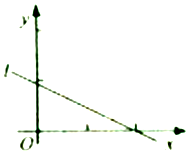 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )| A. | x和y的相关系数在-1和0之间 | |
| B. | x和y的相关系数为直线l的斜率 | |
| C. | 当n为偶数时,分布在l两侧的样本点的个数一定相同 | |
| D. | 所有样本点(xi,yi)(i=1,2,…,n)都在直线l上 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ac>bc,则a>b | B. | 若a>b,c>d,则ac>bd | ||
| C. | 若a>b,则$\frac{1}{a}<\frac{1}{b}$ | D. | 若ac2>bc2,则a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com