
| A�� | ������ƽ�������������λ��һ���������ܲ��� | |
| B�� | ������ƽ�������������λ�����ܲ��䣬������ | |
| C�� | ������ƽ�������������λ�����ܲ��䣬����Ҳ���� | |
| D�� | ������ƽ�������ܲ��䣬��λ�����ܲ��䣬������ܲ��� |
���� ��������x1��x2��x3������xn���人����ְͨ��n��n��3��n��N*�����˵������룬����n�����ݵ���λ��Ϊx��ƽ����Ϊy������Ϊz������ټ�����������������xn+1�����Ǹ���ƽ���������壬��λ���Ķ��壬����������壬�������ڼ���xn+1�����ݵı仯�������õ��𰸣�
��� �⣺������x1��x2��x3������xn���人����ְͨ��n��n��3��n��N*�����˵������룬
��xn+1Ϊ�������������룬��xn+1��Զ����x1��x2��x3������xn��
����n+1�������У�������ƽ�������������λ�����ܲ��䣬Ҳ���������
���������ݵļ��г���Ҳ�ܵ�xn+1�Ƚϴ��Ӱ�죬��������ɢ������
��ѡ��B��
���� ���⿼���֪ʶ���Ƿ��ƽ��������λ������ȷ����ƽ���������壬��λ���Ķ��壬����������壬�ǽ����Ĺؼ������⣬����ʵ�������������xn+1��Զ����x1��x2��x3������xn��Ҳ�ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
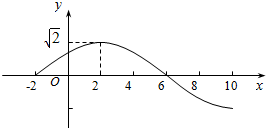 ��֪����f��x��=Asin����x+ϕ����A��0���أ�0��|ϕ|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ��
��֪����f��x��=Asin����x+ϕ����A��0���أ�0��|ϕ|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��1�� | B�� | ��1��-1�� | C�� | ��1��1�� | D�� | ��0��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com