Question

12．已知平行六面体ABCD-A₁B₁C₁D₁，AC₁与平面A₁BD，CB₁D₁交于E，F两点．
以下命题中真命题有①②④_（写出所有正确命题的序号）
①点E，F为线段AC₁的两个三等分点；
②四面体AB₁CD₁的体积是平行六面体ABCD-A₁B₁C₁D₁体积的三分之一；
③E为△A₁BD的内心；
④若∠A₁AB=∠A₁AD=∠BAD，AA₁=AB=AD，则AC₁⊥面A₁BD．

Answer 1

分析 ①在对角面ACC₁A₁中可看出点E，F为线段AC₁的两个三等分点，正确；
②四面体AB₁CD₁可以看作是一个平行六面体裁去四个角，很容易证明是正确的；
③A₁E为△A₁BD的边BD的中线，故E不一定为△A₁BD的内心（实际上是重心），故错误；
④根据线面垂直，推出线线垂直，再推出线面垂直，正确．

解答 解：①如图，在对角面ACC₁A₁中可看出点E，F为线段AC₁的两个三等分点，正确；
②四面体AB₁CD₁可以看作是一个平行六面体裁去四个角，
设平行六面体的边长a，每个角体积为$\frac{{a}^{3}}{6}$，剩下a³-4×$\frac{{a}^{3}}{6}$=$\frac{1}{3}{a}^{3}$，正确；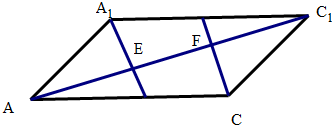
③A₁E为△A₁BD的边BD的中线，故E不一定为△A₁BD的内心（实际上是重心），故错误；
④如图：
BD⊥AC，BD⊥A₁E（两个等腰三角形），
∴BD⊥平面AA₁C₁C，
∵AC₁∈AA₁C₁C，
∴AC₁⊥BD；
同理可证 AC₁⊥A₁B AC₁⊥A₁D，
可证AC₁⊥平面A₁BD．
故答案为：①②④．

点评 本题考查了平行六面体的结构特征、重心、线面垂直的证明方法，属于中档题．