已知a.b∈R.则“ab＞0“是“$\frac{b}{a}$+$\frac{a}{b}$＞2 的( )A．充分非必要条件B．必要非充分条件C．充要条件D．既非充分也非必要条件题目和参考答案——青夏教育精英家教网—

19．已知a，b∈R，则“ab＞0“是“$\frac{b}{a}$+$\frac{a}{b}$＞2”的（　　）

	A．	充分非必要条件		B．	必要非充分条件
	C．	充要条件		D．	既非充分也非必要条件

分析根据充分必要条件的定义判断即可．

解答解：由$\frac{b}{a}$+$\frac{a}{b}$＞2，得：$\frac{{（a-b）}^{2}}{ab}$＞0，
故ab＞0且a≠b，
故“ab＞0“是“$\frac{b}{a}$+$\frac{a}{b}$＞2”的必要不充分条件，
故选：B．

点评本题考查了充分必要条件，考查不等式问题，是一道基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

9．解关于x的不等式：
①x²-5x-6＜0
②$\frac{x-1}{x+2}$≤0．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．

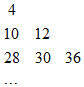设数列{a_n}是集合{x|x=3^s+3^t，s＜t且s，t∈N}中所有的数从小到大排列成的数列，即a₁=4，a₂=10，a₃=12，a₄=28，a₅=30，a₆=36，…，将数列{a_n}中各项按照上小下大，左小右大的原则排成如图的等腰直角三角形数表，则a₁₅的值为324．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

7．

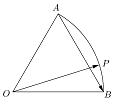如图，已知半径为1的扇形AOB，∠AOB=60°，P为弧$\widehat{AB}$上的一个动点，则$\overrightarrow{OP}•\overrightarrow{AB}$取值范围是[$-\frac{1}{2}$，$\frac{1}{2}$]．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．

如图所示，沿河有A、B两城镇，它们相距20千米，以前，两城镇的污水直接排入河里，现为保护环境，污水需经处理才能排放，两城镇可以单独建污水处理厂，或者联合建污
水处理厂（在两城镇之间或其中一城镇建厂，用管道将污水从各城镇向污水处理厂输送），依据经验公式，建厂的费用为f（m）=25•m^0.7（万元），m表示污水流量，铺设管道的费用（包括管道费）$g（x）=3.2\sqrt{x}$（万元），x表示输送污水管道的长度（千米）；
已知城镇A和城镇B的污水流量分别为m₁=3、m₂=5，A、B两城镇连接污水处理厂的管道总长为20千米；假定：经管道运输的污水流量不发生改变，污水经处理后直接排入河中；请解答下列问题（结果精确到0.1）
（1）若在城镇A和城镇B单独建厂，共需多少总费用？
（2）考虑联合建厂可能节约总投资，设城镇A到拟建厂的距离为x千米，求联合建厂的总费用y与x的函数关系
式，并求y的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．已知在二项式${（\root{3}{x}-\frac{1}{{2\root{3}{x}}}）^n}$的展开式中，第6项为常数项．
（1）求n的值，并求含x²项的系数；
（2）求展开式中所有的有理项．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

11．不等式$\frac{（x+4）（x+3）}{{{x^2}-5x+4}}＜0$的解集为（-4，-3）∪（1，4）．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

8．在平面直角坐标系xOy中，设不等式组$\left\{\begin{array}{l}-1≤x≤2\\ 0≤y≤2\end{array}\right.$所表示的平面区域是W，从区域W中随机取点M（x，y）．
（1）若x，y∈Z，求点M位于第一象限的概率；
（2）若x，y∈R，求|OM|≥1的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

18．对任意的实数x，若[x]表示不超过x的最大整数，则“-1＜x-y＜1”是“[x]=[y]”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学