
分析 由$\overrightarrow{EF}$=$\overrightarrow{EA}$+$\overrightarrow{AB}$+$\overrightarrow{BF}$,两边平方即可解得线段AB的长.
解答 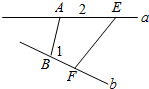 解:如图,由$\overrightarrow{EF}$=$\overrightarrow{EA}$+$\overrightarrow{AB}$+$\overrightarrow{BF}$,得
解:如图,由$\overrightarrow{EF}$=$\overrightarrow{EA}$+$\overrightarrow{AB}$+$\overrightarrow{BF}$,得
由$\overrightarrow{EF}$2=$\overrightarrow{EA}$2+$\overrightarrow{AB}$2+$\overrightarrow{BF}$2+2|$\overrightarrow{EA}$||$\overrightarrow{BF}$|cosθ
①当θ=60°时,有9=4+$\overrightarrow{AB}$2+1+2•2•$\frac{1}{2}$,得|$\overrightarrow{AB}$|=$\sqrt{2}$;
②当θ=120°时,有9=4+$\overrightarrow{AB}$2+1-2•2•$\frac{1}{2}$,得|$\overrightarrow{AB}$|=$\sqrt{6}$.
∴线段AB的长为$\sqrt{2}$或$\sqrt{6}$.
故答案为:$\sqrt{2}$或$\sqrt{6}$.
点评 本题考虑到若用前两种方法都难以奏效,于是选用了“回路法”,更方便了“异面直线a,b所成的角为60°”的讨论与运用,使得解题快捷无比.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,7),(5,2) | B. | (-1,7),(-5,2) | C. | (1,4),(5,2) | D. | (-1,4),(-5,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
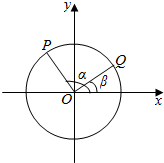 如图,以x轴正半轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q.已知点P(-$\frac{3}{5}$,$\frac{4}{5}$),$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,求:
如图,以x轴正半轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q.已知点P(-$\frac{3}{5}$,$\frac{4}{5}$),$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E为PA的中点,
四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E为PA的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
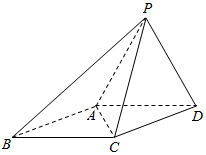 如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
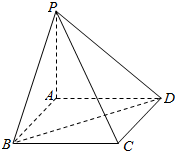 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -$\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | -$\sqrt{2}$ | -1 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com