Question

9．在等腰△ABC中，BD和CE是两腰上的中线，且以BD⊥CE，求cosA．

Answer 1

分析 连接DE，过E点作EF⊥BC，垂足为F，设DE=2x，DE为△ABC的中位线，故BC=4x，四边形BCDE为等腰梯形，根据等腰梯形的性质可知，BF=$\frac{1}{2}$（BC-DE）=x，则FC=3x，又△BCG为等腰直角三角形，故△CEF为等腰直角三角形，则EF=CF=3x，解Rt△BEF可求解cos∠BEF，利用二倍角公式可得顶角∠A的余弦值．

解答 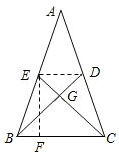解：如图，连接DE，过E点作EF⊥BC，垂足为F，设DE=2x，
依题意，得DE为△ABC的中位线，∴BC=4x，
又∵四边形BCDE为等腰梯形，
∴BF=$\frac{1}{2}$（BC-DE）=x，则FC=3x，
∵BD⊥CE，
∴△BCG为等腰直角三角形，
∵EF⊥BC，
∴△CEF为等腰直角三角形，
∴EF=CF=3x，
在Rt△BEF中，EF=3x，BF=x，BE=$\sqrt{10}$x，
∴cos∠BEF=$\frac{\sqrt{3}}{10}$，
∴cos∠A=2cos²∠BEF-1=2×$\frac{9}{10}$-1=$\frac{4}{5}$．

点评 本题考查了锐角三角函数值的求法，三角形中位线定理，梯形的性质．求锐角的三角函数值的方法：利用锐角三角函数的定义，通过设参数的方法，把问题转化到直角三角形中求三角函数值．