
分析 (1)由题意可知:将直线y=x+1代入抛物线方程,由△=0,即可求得p的值,求得抛物线C的方程;
(2)假设存在常数λ,使得|PM|2=λ|PA||PB|成立,由(1)求得M坐标,|PM|2=2m2,求得直线的斜率,设直线方程为y=2x+m(m≠0),代入抛物线方程,由韦达定理及向量数量积的坐标表示可知:丨PA丨丨PB丨=$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\frac{5}{4}$m2,则2m2=$\frac{5}{4}$m2λ,即可求得常数λ.
解答 解:(1)由题意可知:$\left\{\begin{array}{l}{y=x+1}\\{{y}^{2}=2px}\end{array}\right.$,整理得:x2+2(1-p)x+1=0,
由抛物线C:y2=2px(p>0)与直线l:x-y+1=0相切,
∴△=0,即4(1-p)2-4=0,解得:p=2或p=0(舍去),
∴抛物线方程为:y2=4x;
(2)假设存在常数λ,使得|PM|2=λ|PA||PB|成立,
由(1)可知:M(1,2),则kOM=2,
设直线l′方程为y=2x+m(m≠0),
A(x1,y1),B(x2,y2),
则P(1-m,2-m),|PM|2=2m2,
则$\left\{\begin{array}{l}{y=2x+m}\\{{y}^{2}=4x}\end{array}\right.$,整理得:4x2+4(m-1)x+m2=0,
由△>0,即16(m-1)2-16m2>0,解得:m<$\frac{1}{2}$且m≠0,
由韦达定理可知:x1+x2=1-m,x1•x2=$\frac{{m}^{2}}{4}$,
由丨PA丨丨PB丨=$\overrightarrow{PA}$•$\overrightarrow{PB}$=5[x1•x2+(m-1)(x1+x2)+(m-1)2]=$\frac{5}{4}$m2,
整理得:2m2=$\frac{5}{4}$m2λ,解得:λ=$\frac{8}{5}$,
∴存在常数λ=$\frac{8}{5}$,使得|PM|2=λ|PA||PB|成立.
点评 本题考查抛物线的标准方程,直线与抛物线的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{10}$,1) | B. | (0,$\frac{1}{10}$)∪(1,+∞) | C. | ($\frac{1}{10}$,10) | D. | (0,1)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
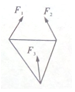 如图,一块均匀的正三角形面的钢板的质量为10$\sqrt{6}$kg,在它的顶点处分别受力F1,F2,F3,每个力同它相邻的三角形的两边之间的角都是60°,且|F1|=|F2|=|F3|.要提起这块钢板,|F1|,|F2|,|F3|均要大于xkg,则x的最小值为$\frac{20\sqrt{2}}{3}$.
如图,一块均匀的正三角形面的钢板的质量为10$\sqrt{6}$kg,在它的顶点处分别受力F1,F2,F3,每个力同它相邻的三角形的两边之间的角都是60°,且|F1|=|F2|=|F3|.要提起这块钢板,|F1|,|F2|,|F3|均要大于xkg,则x的最小值为$\frac{20\sqrt{2}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,6} | B. | {4,5} | C. | {2,4,5} | D. | {2,4,5,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数f(x)=sin(ωx+φ)(其中ω>0且|φ|≤$\frac{π}{2}$)的图象如图所示,为了得到y=sinωx的图象,只需把y=f(x)的图象上所有点( )
函数f(x)=sin(ωx+φ)(其中ω>0且|φ|≤$\frac{π}{2}$)的图象如图所示,为了得到y=sinωx的图象,只需把y=f(x)的图象上所有点( )| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{3}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com