
| A. | ?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数 | |
| B. | ?α,β∈R,使cos(α+β)=cosα+cosβ | |
| C. | 向量$\overrightarrow a=(2,-1)$,$\overrightarrow b=(-3,0)$,则$\overrightarrow a$在$\overrightarrow b$方向上的投影为-2 | |
| D. | “|x|≤1”是“x<1”的既不充分又不必要条件 |
分析 逐项分析,即可得解.A,当φ=$\frac{π}{2}$,时,f(x)=cos2x是偶函数,故A为假.BCD三选项以判断都正确.
解答 解:A、当φ=$\frac{π}{2}$,时,f(x)=cos2x是偶函数,故A为假;
B、取$α=\frac{3π}{4},β=-\frac{π}{4}$,此时$cos(\frac{3π}{4}-\frac{π}{4})=cos\frac{3π}{4}+cos(-\frac{π}{4})=0$,故B正确;
C、根据向量数量积的几何意义知,向量$\overrightarrow{a}在\overrightarrow{b}$上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}=\frac{-6}{3}=-2$,故C正确;
D、当|x|≤1时,可得-1≤x≤1,此时不能推出x<1,故|x|≤1不是x<1的充分条件;当x<1时,取x=-2,此时|x|=2>1,所以x<1不能推出|x|≤1,故|x|≤1也不是x<1的必要条件.故|x|≤1是x<1的既不充分也不必要条件.
故选A.
点评 本题考查了命题真假的判断,向量数量积的几何意义及充分必要条件的判断.正确掌握基本知识和基本方法是解题的关键.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x(x-1) | B. | x(x+1) | C. | -x(x-1) | D. | -x(x+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
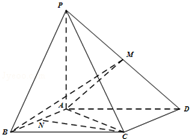 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com