
| A. | (-$\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$) | B. | (-$\frac{3\sqrt{2}}{2}$,-$\frac{3}{2}$] | C. | (-$\sqrt{2}$,$\sqrt{2}$) | D. | (-$\sqrt{2}$,-1] |
分析 由题意求出曲线的普通方程,结合直线与曲线的图形,求出满足题意的b的范围即可.
解答 解:曲线$\left\{\begin{array}{l}{x=\frac{3}{2}cosθ}\\{y=\frac{3}{2}sinθ}\end{array}\right.$(θ为参数,且-$\frac{π}{2}$≤θ≤$\frac{π}{2}$),化为:x2+y2=$\frac{9}{4}$(x≥0),表示以原点为圆心,$\frac{3}{2}$为半径的右半圆,
直线y=x+b与$\left\{\begin{array}{l}{x=\frac{3}{2}cosθ}\\{y=\frac{3}{2}sinθ}\end{array}\right.$(θ为参数,且-$\frac{π}{2}$≤θ≤$\frac{π}{2}$)有两个不同的交点,
过(0,-$\frac{3}{2}$)时,b=-$\frac{3}{2}$;直线与半圆相切时,b=-$\frac{3\sqrt{2}}{2}$
所以实数b的取值范围是(-$\frac{3\sqrt{2}}{2}$,-$\frac{3}{2}$].
故选B.
点评 本题是中档题,考查参数方程与普通方程的求法,考查数形结合的思想,直线的截距的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,5] | B. | [1,5] | C. | (0,5) | D. | [1,25] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
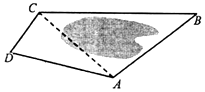 如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD的各边的AB=5,BC=8,CD=3,DA=5长度(单位:km):,如图所示,若A、B、C、D四点共圆.
如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD的各边的AB=5,BC=8,CD=3,DA=5长度(单位:km):,如图所示,若A、B、C、D四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com