
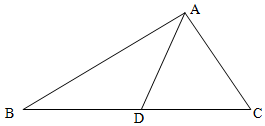
 如图所示,MCN是某海湾旅游区的一角,为营造更加优美的旅游环境,旅游区管委会决定建立面积为4$\sqrt{3}$平方千米的三角形主题游戏乐园ABC,并在区域CDE建立水上餐厅.已知∠ACB=120°,∠DCE=30°.
如图所示,MCN是某海湾旅游区的一角,为营造更加优美的旅游环境,旅游区管委会决定建立面积为4$\sqrt{3}$平方千米的三角形主题游戏乐园ABC,并在区域CDE建立水上餐厅.已知∠ACB=120°,∠DCE=30°.分析 (Ⅰ)设AC=x,AB=y,利用余弦定理求得BC的值,可得y的解析式,再利用基本不等式求得y的最小值.
(Ⅱ)△ACD中,由正弦定理求得CD的值,△ACE中,由正弦定理可得CE的值,根据区域CDE的面积S=$\frac{1}{2}$•CD•CE•sin30°,利用正弦函数的值域求得区域CDE的面积S的最小值.
解答 解:(Ⅰ)∵AC=x,AB=y,∠ACB=120°,
S△ABC=$\frac{1}{2}$•AC•BC•sin120°=$\frac{1}{2}•x•BC•\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,
∴BC=$\frac{16}{x}$.
△ABC中,利用余弦定理可得AB2=AC2+BC2-2AC•BC•cos120°,
即y2=x2+$\frac{256}{{x}^{2}}$+16≥2$\sqrt{{x}^{2}•\frac{256}{{x}^{2}}}$+16=48,
∴y≥4$\sqrt{3}$,当且仅当x2=16,即x=4时,取等号,
故当x=4时,y取得最小值为4$\sqrt{3}$.
(Ⅱ)设∠ACD=θ(θ为锐角),
当AB最小时,x=AC=4=BC,AB=4$\sqrt{3}$,∠CAB=∠CBA=30°,
△ACD中,由正弦定理可得$\frac{CD}{sin∠CAB}$=$\frac{AC}{sin∠CDA}$,
∴CD=$\frac{AC•sin∠CAB}{sin∠CDA}$=$\frac{4sin30°}{sin(150°-θ)}$=$\frac{2}{sin(150°-θ)}$,
△ACE中,由正弦定理可得CE=$\frac{AC•sin∠CAE}{sin∠CEA}$=$\frac{4sin30°}{sin(120°-θ)}$=$\frac{2}{sin(120°-θ)}$,
根据区域CDE的面积S=$\frac{1}{2}$•CD•CE•sin30°=$\frac{1}{sin(150°-θ)•sin(120°-θ)}$=$\frac{4}{\sqrt{3}+2sin2θ}$,
故当2θ=$\frac{π}{2}$,即θ=$\frac{π}{4}$时,区域CDE的面积S取得最小值为$\frac{4}{\sqrt{3}+2}$=8-4$\sqrt{3}$.
点评 本题主要考查余弦定理、正弦定理、基本不等式的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 5 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,5} | B. | {-1,0,1} | C. | {0,1} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com