Question

2．如图，在△ABC中，角A，B，C所对的边分别为a，b，c，且2acosC-2b=c．
（1）求角A的大小；
（2）若AD是∠BAC的角平分线，$AB=4\sqrt{3}，AC=2\sqrt{3}$，求BD的长．

Answer 1

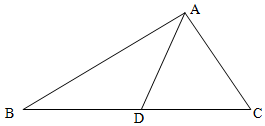
分析 （1）利用正弦定理、诱导公式、两角和的正弦公式求得cosA=-$\frac{1}{2}$，可得A的值．
（2）△ABC中，由余弦定理求得BC的值，再利用三角形内角平分线的性质，求得BD的值．

解答 解：（1）∵2acosC-c=2b，由正弦定理得2sinAcosC-sinC=2sinB，
即 2sinAcosC-sinC=2sin（A+C）=2sinAcosC+2cosAsinC，
∴-sinC=2cosAsinC，∵sinC≠0，∴cosA=-$\frac{1}{2}$，
而A∈（0，π），∴A=$\frac{2π}{3}$．
（2）在△ABC中，由余弦定理得，
BC²=AB²+AC²-2AB•AC•cos$\frac{2π}{3}$=48+12-2•4$\sqrt{3}$•2$\sqrt{3}$•（-$\frac{1}{2}$）=84，
∴BC=2$\sqrt{21}$．
∵AD是∠BAC的角平分线，∴$\frac{BD}{CD}$=$\frac{AB}{AC}$=2，∴BD=$\frac{2}{3}$BC=$\frac{4\sqrt{21}}{3}$．

点评 本题主要考查正弦定理、余弦定理的应用，三角形内角平分线的性质，属于中档题．