
分析 (Ⅰ)求得导数,代入x=1,解方程可得a;
(Ⅱ)由题意可得xlnx-x2-2mx≤0恒成立,即:$m≥\frac{1}{2}lnx-\frac{1}{2}x$恒成立,令$h(x)=\frac{1}{2}lnx-\frac{1}{2}x$,求出h(x)的导数,单调区间,求得最大值,即可得到m的取值范围;
(Ⅲ)要证明函数y=f(x)+2x的图象在g(x)=xex-x2-1图象的下方,即证:f(x)+2x<xex-x2-1恒成立,即证lnx≤x-1,即证:ex-x-1>0,令φ(x)=ex-x-1,求得导数,得到单调性,即可得证.
解答 解:(Ⅰ)易知f'(x)=lnx+1+ax,
所以f'(1)=1+a,又f'(1)=-1…(1分)
∴a=-2…(2分)
∴f(x)=xlnx-x2-1.…(3分)
(Ⅱ)若对任意的x∈(0,+∞),都有f(x)-2mx+1≤0,
即xlnx-x2-2mx≤0恒成立,即:$m≥\frac{1}{2}lnx-\frac{1}{2}x$恒成立…(4分)
令$h(x)=\frac{1}{2}lnx-\frac{1}{2}x$,则$h'(x)=\frac{1}{2x}-\frac{1}{2}=\frac{1-x}{2x}$,…(6分)
当0<x<1时,$h'(x)=\frac{1-x}{2x}>0$,所以h(x)单调递增;
当x>1时,$h'(x)=\frac{1-x}{2x}<0$,所以h(x)单调递减;…(8分)
∴x=1时,h(x)有最大值$h(1)=-\frac{1}{2}$,
∴$m≥-\frac{1}{2}$,即m的取值范围为$[-\frac{1}{2},+∞)$.…(10分)
(Ⅲ)证明:要证明函数y=f(x)+2x的图象在g(x)=xex-x2-1图象的下方,
即证:f(x)+2x<xex-x2-1恒成立,
即:lnx<ex-2…(11分)
由(Ⅱ)可得:$h(x)=\frac{1}{2}lnx-\frac{1}{2}x≤-\frac{1}{2}$,所以lnx≤x-1,
要证明lnx<ex-2,只要证明x-1<ex-2,即证:ex-x-1>0…(12分)
令φ(x)=ex-x-1,则φ'(x)=ex-1,
当x>0时,φ'(x)>0,所以φ(x)单调递增,
∴φ(x)>φ(0)=0,
即ex-x-1>0,…(13分)
所以x-1<ex-2,从而得到lnx≤x-1<ex-2,
所以函数y=f(x)+2x的图象在g(x)=xex-x2-1图象的下方.…(14分)
点评 本题考查导数的运用:求单调区间和极值、最值,考查恒成立思想的运用和参数分离方法,以及构造函数法,注意运用分析法证明不等式,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{2}$ | B. | 9 | C. | $\frac{29}{3}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
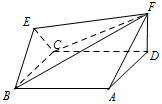 如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=1-lg|x| | B. | $y=lg\frac{x-1}{x+1}$ | C. | $y=\frac{x+1}{x-1}-\frac{x-1}{x+1}$ | D. | $y=\frac{|x|}{x+1}+\frac{|x|}{x-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com