
分析 设斜率为1的直线为y=x+t,代入椭圆方程x2+4y2=4,运用判别式大于0和韦达定理,弦长公式,化简整理,由二次函数的最值的求法,即可得到最大值.
解答 解:设斜率为1的直线为y=x+t,代入椭圆方程x2+4y2=4,可得
5x2+8tx+4t2-4=0,
设A(x1,y1),B(x2,y2),
可得判别式为64t2-80(t2-1)>0,
解得-$\sqrt{5}$<t<$\sqrt{5}$,
x1+x2=-$\frac{8t}{5}$,x1x2=$\frac{4{t}^{2}-4}{5}$,
弦长|AB|=$\sqrt{2}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{2}$•$\sqrt{\frac{64{t}^{2}}{25}-\frac{16({t}^{2}-1)}{5}}$=$\frac{4\sqrt{2}}{5}$•$\sqrt{5-{t}^{2}}$≤$\frac{4\sqrt{10}}{5}$.
当t=0时,|AB|取得最大值$\frac{4\sqrt{10}}{5}$.
故答案为:$\frac{4\sqrt{10}}{5}$.
点评 本题考查直线方程和椭圆方程联立,运用判别式大于0和韦达定理,以及弦长公式,考查二次函数的最值的求法,属于中档题.


科目:高中数学 来源: 题型:解答题
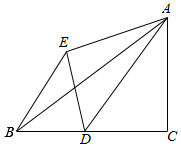 如图,△ABC中,∠C=90°,AC=6,BC=8,点D从点C出发,以每秒1个单位的速度沿着CB向点B运功,△ADE和△ADC关于AD成轴对称,连接BE,设点D运动时间为t秒.
如图,△ABC中,∠C=90°,AC=6,BC=8,点D从点C出发,以每秒1个单位的速度沿着CB向点B运功,△ADE和△ADC关于AD成轴对称,连接BE,设点D运动时间为t秒.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.3750 | B. | 0.3000 | C. | 0.2500 | D. | 0.2000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,e] | B. | $(1+\frac{1}{e},e]$ | C. | (1,e] | D. | $[1+\frac{1}{e},e]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 61 | C. | 62 | D. | 63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com