练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．设集合U={1，2，3，4}，A={1，2}，B={2，4}，则（∁UA）∩B={4}．

    分析 根据题意，先求出A的补集∁UA，再由交集的意义，计算可得（∁UA）∩B，即可得答案．

    解答 解：∵集合U={1，2，3，4}，A={1，2}，B={2，4}，
    ∴∁UA={3，4}，
    ∴（∁UA）∩B={4}，
    故答案为：{4}．

    点评 本题考查集合混合运算，注意运算的顺序，其次要理解集合交、并、补的含义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

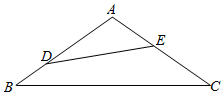    17．某小区要将如图所示的一块三角形边角地修建成花圃．根据建造规划，要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分（其中D在边AB上，E在边AC上）已知AB=AC=2a，∠BAC=120°
    （1）设AD=x，DE=y，试求y关于x的函数y=f（x）（解析式和定义域）；
    （2）为使得灌溉水道DE的建设费用最少，试确定点D的具体位置．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知数列{an}为等差数列，满足$\left\{\begin{array}{l}2≤{a_1}+2{a_2}≤4\\-1≤2{a_2}+3{a_3}≤1\end{array}\right.$，则当a4取最大值时，数列{an}的通项公式为an=$-\frac{1}{2}n+\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．过抛物线y2=2x焦点的直线交抛物线于A、B两点，且|AB|=4，则线段AB中点M的横坐标为$\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．某家电商场开展购物抽奖促销活动，顾客购物满500元即可获得一次抽奖机会，若每10张券中有一等奖券1张，可获价值100元的奖品；有二等奖券3张，每张可获价值50元的奖品；其余6张没有奖，某顾客从这10张券中任抽2张，求：
    （Ⅰ）该顾客中奖的概率；
    （Ⅱ）该顾客获得的奖品总价值ξ（元）的概率分布列和期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．使得2x-14＜$\sqrt{x}$＜log2x成立的x的范围是（4，16）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知数列{an}的前n项和为Sn，且an=2+（-$\frac{1}{3}$）n-1，若对任意的n∈N*，都有1≤p（Sn-2n）≤3，则实数p的取值范围是$[\frac{3}{2}，3]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．请阅读问题1的解答过程，然后借鉴问题1的解题思路完成问题2的解答：
    问题1：已知数集A={a1，a2，…an}（1≤a1＜a2＜…＜an，n≥2）具有性质P：对任意的i，j（1≤i≤j≤n），aiaj与$\frac{a_j}{a_i}$两数中至少有一个属于A．若数集{a1，2，3，a4}具有性质P，求a1，a4的值．
    解：对于集合中最大的数a4，因为a4×a4＞a4，3×a4＞a4，2×a4＞a4．
    所以$\frac{a_4}{a_4}$，$\frac{a_4}{3}$，$\frac{a_4}{2}$都属于该集合．
    又因为1≤a1＜2＜3＜a4，所以$\frac{a_4}{a_4}＜\frac{a_4}{3}＜\frac{a_4}{2}＜{a_4}$．
    所以${a_1}=\frac{a_4}{a_4}=1$，$\frac{a_4}{3}=2，\frac{a_4}{2}=3$，故a1=1，a4=6．
    问题2：已知数集A={a1，a2，…an}（0≤a1＜a2＜…＜an，n≥2）具有性质P：
    对任意的i，j（1≤i≤j≤n），ai+aj与aj-ai两数中至少有一个属于A．若数集{a1，1，3，a4}具有性质P，求a1，a4的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．化简sin10°cos50°+cos10°sin50°=$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    同步练习册答案