
【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标是ρ=2asinθ,直线l的参数方程是  (t为参数).
(t为参数).
(1)若a=2,M为直线l与x轴的交点,N是圆C上一动点,求|MN|的最大值;
(2)若直线l被圆C截得的弦长为 ![]() ,求a的值.
,求a的值.
【答案】
(1)解:直线l的参数方程是  ,a=2时,化为普通方程:
,a=2时,化为普通方程: ![]() (x﹣2).令y=0,解得x=2,可得M(2,0).圆C的极坐标是ρ=2asinθ,即ρ2=4ρsinθ,可得直角坐标方程:x2+y2﹣4y=0,即x2+(y﹣2)2=4.
(x﹣2).令y=0,解得x=2,可得M(2,0).圆C的极坐标是ρ=2asinθ,即ρ2=4ρsinθ,可得直角坐标方程:x2+y2﹣4y=0,即x2+(y﹣2)2=4.
|MC|=2 ![]() ,∴|MN|的最大值为2
,∴|MN|的最大值为2 ![]() +2
+2
(2)解:圆C的方程为:x2+(y﹣a)2=a2,直线l的方程为:4x+3y﹣4a=0,
圆心C到直线l的距离d= ![]() =
= ![]() .
.
∴ ![]() =2
=2 ![]() ,解得a=
,解得a= ![]()
【解析】(1)直线l的参数方程是  ,a=2时,化为普通方程:
,a=2时,化为普通方程: ![]() (x﹣2).可得M(2,0).圆C的极坐标是ρ=2asinθ,即ρ2=4ρsinθ,利用互化公式可得直角坐标方程,求出|MC|=2
(x﹣2).可得M(2,0).圆C的极坐标是ρ=2asinθ,即ρ2=4ρsinθ,利用互化公式可得直角坐标方程,求出|MC|=2 ![]() ,可得|MN|的最大值为2
,可得|MN|的最大值为2 ![]() +r.(2)圆C的方程为:x2+(y﹣a)2=a2,直线l的方程为:4x+3y﹣4a=0,利用点到直线的距离公式与弦长公式即可得出.
+r.(2)圆C的方程为:x2+(y﹣a)2=a2,直线l的方程为:4x+3y﹣4a=0,利用点到直线的距离公式与弦长公式即可得出.


科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AB=2,AD=1点E,F,G分别是DD1 , AB,CC1的中点,则异面直线A1E与GF所成的角是( ) 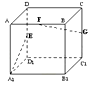
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根据上表可得回归直线方程 ![]() ,其中
,其中 ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,据此估计,该社区一户居民年收入为15万元家庭的年支出为万元.
,据此估计,该社区一户居民年收入为15万元家庭的年支出为万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读与探究
人教A版《普通高中课程标准实验教科书 数学4(必修)》在第一章的小结中写到:
将角放在直角坐标系中讨论不但使角的表示有了统一的方法,而且使我们能够借助直角坐标系中的单位圆,建立角的变化与单位圆上点的变化之间的对应关系,从而用单位圆上点的纵坐标、横坐标来表示圆心角的正弦函数、余弦函数.因此,正弦函数、余弦函数的基本性质与圆的几何性质(主要是对称性)之间存在着非常紧密的联系.例如,和单位圆相关的“勾股定理”与同角三角函数的基本关系有内在的一致性;单位圆周长为![]() 与正弦函数、余弦函数的周期为
与正弦函数、余弦函数的周期为![]() 是一致的;圆的各种对称性与三角函数的奇偶性、诱导公式等也是一致的等等.因此,三角函数的研究过程能够很好地体现数形结合思想.
是一致的;圆的各种对称性与三角函数的奇偶性、诱导公式等也是一致的等等.因此,三角函数的研究过程能够很好地体现数形结合思想.

依据上述材料,利用正切线可以讨论研究得出正切函数![]() 的性质.
的性质.
比如:由图1.2-7可知,角![]() 的终边落在四个象限时均存在正切线;角
的终边落在四个象限时均存在正切线;角![]() 的终边落在
的终边落在![]() 轴上时,其正切线缩为一个点,值为
轴上时,其正切线缩为一个点,值为![]() ;角
;角![]() 的终边落在
的终边落在![]() 轴上时,其正切线不存在;所以正切函数
轴上时,其正切线不存在;所以正切函数![]() 的定义域是
的定义域是![]() .
.
(1)请利用单位圆中的正切线研究得出正切函数![]() 的单调性和奇偶性;
的单调性和奇偶性;
(2)根据阅读材料中途1.2-7,若角![]() 为锐角,求证:
为锐角,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,E、F分别是棱DD1、C1D1的中点. 
(Ⅰ)证明:平面ADC1B1⊥平面A1BE;
(Ⅱ)证明:B1F∥平面A1BE;
(Ⅲ)若正方体棱长为1,求四面体A1﹣B1BE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点(0,1)的直线与圆x2+y2=4相交于A、B两点,若 ![]() ,则点P的轨迹方程是( )
,则点P的轨迹方程是( )
A.![]()
B.x2+(y﹣1)2=1
C.![]()
D.x2+(y﹣1)2=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A是抛物线M:y2=2px(p>0)与圆C:x2+(y﹣4)2=a2在第一象限的公共点,且点A到抛物线M焦点F的距离为a,若抛物线M上一动点到其准线与到点C的距离之和的最小值为2a,O为坐标原点,则直线OA被圆C所截得的弦长为( )
A.2
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com