练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在平面直角坐标系中，已知O（0，0）、A（2，3）、B（-4，7），则向量
    OA
    在向量
    OB
    方向上的投影等于
     
    ．
    考点：平面向量数量积的运算
    专题：计算题,平面向量及应用
    分析：运用向量的模的公式和数量积的坐标表示，结合向量
    OA
    在向量
    OB
    方向上的投影为
    OA
    •
    OB
    |
    OB
    |
    ，计算即可得到．
    解答： 解：由于O（0，0）、A（2，3）、B（-4，7），
    则
    OA
    =（2，3），
    OB
    =（-4，7），
    OA
    •
    OB
    =2×（-4）+3×7=13，
    |
    OB
    |=
    		16+49
    =
    		65
    ，
    则向量
    OA
    在向量
    OB
    方向上的投影为
    OA
    •
    OB
    |
    OB
    |
    =
    13
    		65
    =
    		65
    5
    ．
    故答案为：
    		65
    5
    ．
    点评：本题考查向量的数量积的坐标表示和向量的模的公式，考查向量的投影的概念，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在平面直角坐标系中，以坐标原点为极点，以x轴正半轴为极轴，建立极坐标系，得到曲线C的极坐标方程是ρ=4sinθ
    （Ⅰ）写出曲线C的标准方程及其参数方程；
    （Ⅱ）在平面直角坐标系中，对于两点P（x1，y1），Q（x2，y2），记δ=|x1-x2|+|y1-y2|，点P（2，4），Q在曲线C上运动，求δ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    观察下列式子：1+
    1
    22
    ＜
    3
    2
    ，1+
    1
    22
    +
    1
    32
    ＜
    5
    3
    ，1+
    1
    2 
    +
    1
    32
    +
    1
    42
    ＜
    7
    4
    ，…根据以上式子可以猜想：1+
    1
    22
    +
    1
    32
    +
    1
    42
    +…+
    1
    20152
    ＜
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    把正整数排列陈如图甲的三角形数阵，然后擦去第偶数行中的奇数和第奇数行中的偶数，得到如图乙的三角形数阵，再把图乙中的数按从小到大的顺序排出一列，得到数列{an}．

    （1）a32=
     
    ；
    （2）若an=2080，则n
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    过双曲线
    x2
    3
    -y2=1的两焦点作实轴的垂线，分别与渐近线交于A、B、C、D四点．则矩形ABCD的面积为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

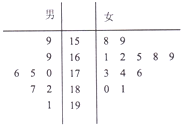    第117届中国进出口商品交易会（简称2015年春季交广会）将于2015年4月15日在广州市举行，为了搞好接待工作，组委会在广州某大学分别招募8名男志愿者和12名女志愿者，现将这20名志愿者的身高组成如茎叶图（单位：m），若身高在175cm以上（包括175cm）定义为“高个子”，身高在175cm以下（不包括175cm）定义为“非高个子”．
    （1）计算男志愿者的平均身高（保留一位小数）；
    （2）如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人，再从这5个人选2人，求至少有1人是“高个子”的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列四个函数：①y=x+1；②y=x-1；③y=x2-1；④y=
    1
    x
    ，其中定义域与值域相同的是（　　）
    A、①②③B、①②④
    C、②③D、②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若直线l1，l2的方向向量分别为
    v1
    =（1，2，3），
    v2
    =（-
    1
    2
    ，-1，-
    3
    2
    ），则l1，l2的位置关系是（　　）
    A、垂直B、重合
    C、平行D、平行或重合

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    斜率为2的直线l过双曲线C：
    x2
    a2
    -
    y2
    b2
    =1（a＞0，b＞0）的右焦点，且与双曲线的左右两支都相交，则双曲线的离心率e的取值范围是（　　）
    A、[2，+∞）
    B、（1，
    		3
    ）
    C、(1，
    		5
    )
    D、（
    		5
    ，+∞）

    查看答案和解析>>

    同步练习册答案