考点:等比数列的性质
专题:等差数列与等比数列
分析:先假设存在正数k使数列{bn}为等差数列,设等比数列{an}的公比为q求出an,代入bn利用对数的运算律、等比数列的通项公式化简bn,再根据等差数列的定义得
bn-bn-1=d(d为常数),再代入bn化简判断出lgk=0,进而求出k的值.
解答:
解:假设存在正数k使数列{b
n}为等差数列,
设等比数列{a
n}的公比为q,则a
n=a
1q
n-1>0,
所以b
n=
[lga
1+lga
2+…+lga
n-1+lg(ka
n)]
=
lg[k(a
1a
2…a
n)]
=
lg[k(a1nq1+2+…+n-1)]=
[lg(ka1n)+lgq]=
[lg(ka1n)+lgq]=
lgk+
lga1+lgq,
如果b
n为等差数列,则有b
n-b
n-1=d(d为常数),n≥2,
所以b
n-b
n-1=
lgk+lga1+lgq-(
lgk+lga1+lgq)
=
lgq-lgk为常数,
因为
不可能为常数,所以系数lgk必为0,即lgk=0,
解得k=1.
则等差数列{b
n}的公差是
lgq,
所以存在这样的k使得数列{bn}成等差数列,且k=1.
点评:本题考查等比数列的通项公式,等差数列的定义以及对数的运算律,较综合,考查计算化简能力.



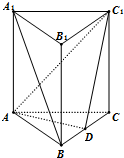 直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,AA1=4,D为BC中点,
直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,AA1=4,D为BC中点,