
分析 根据集合相等的条件和题意分类讨论,分别求出对应的x、y、z的值再验证,最后将代入式子求值即可.
解答 解:由题意知,{x,y,z}={0,1,2},且下列三个关系:①x≠2;②y=2;③z≠0有且只有一个正确,
(1)当①x≠2正确,②y=2、③z≠0不正确时,
有:①x=1,②y=2,③z=0,这与②y=2不正确矛盾,舍去;
(2)当②y=2正确,①x≠2;③z≠0时不正确时,
有:①x=2;②y=2;③z=0,与集合的互异性矛盾,舍去;
(3)当③z≠0正确,②y=2;①x≠2不正确时,
有:①x=2;②y=0;③z=1,满足条件,故成立,
综上可得,满足条件对应的x=2、y=0、z=1,
所以100x+10y+z=201,
故答案为:201.
点评 本题考查了集合相等的条件,集合元素的性质,以及分类讨论思想,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
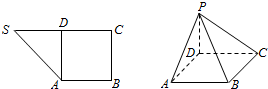 如图1,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.
如图1,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x-3y-19=0 | B. | 4x+3y-13=0 | C. | 3x-4y-16=0 | D. | 3x+4y-8=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=$\frac{π}{2}$,AD=2$\sqrt{2}$,AB=3DC=3.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=$\frac{π}{2}$,AD=2$\sqrt{2}$,AB=3DC=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com