
分析 命题p:由-x2+2x+3>0,解出即可得出函数f(x)=ln(-x2+2x+3)的定义域;
命题q:函数f(x)=ln(-x2+2x+3)的定义域为(-1,3),由函数y=-x2+2x+3=-(x-1)2+4,利用二次函数与对数函数的单调性即可得出.
解答 解:命题p:由-x2+2x+3>0,解得-1<x<3,可得:函数f(x)=ln(-x2+2x+3)的定义域为(-1,3);
命题q:函数f(x)=ln(-x2+2x+3)的定义域为(-1,3),由函数y=-x2+2x+3=-(x-1)2+4,∴函数f(x)=ln(-x2+2x+3)的单调递减区间为(1,3),因此是假命题.
那么命题p为真命题,p∧q为假命题.
故答案分别为:真;假.
点评 本题考查了函数的定义域及其单调性、不等式的解法,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
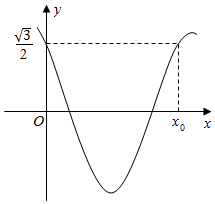 已知函数f(x)=2cosπx•cos2$\frac{φ}{2}$+sin[(x+1)π]•sinφ-cosπx(0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=2cosπx•cos2$\frac{φ}{2}$+sin[(x+1)π]•sinφ-cosπx(0<φ<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<1} | B. | {x|0<x≤1} | C. | {x|0<x<2} | D. | {x|x≤1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com