
| A. | 0条 | B. | 1条 | C. | 2条 | D. | 3条 |
分析 由方程组$\left\{\begin{array}{l}{y=-\frac{1}{3}x+\frac{10}{3}}\\{y=3x}\end{array}\right.$,解得两条直线的交点为A(1,3),当直线的斜率存在时,设所求直线的方程为:y-3=k(x-1),由点到直线的距离公式,求出直线方程为:4x-3y+5=0.当直线的斜率不存在时,直线的方程为x=1也符合题意,故满足条件的直线有2条.
解答 解:由方程组$\left\{\begin{array}{l}{y=-\frac{1}{3}x+\frac{10}{3}}\\{y=3x}\end{array}\right.$,解得两条直线的交点为(1,3),
当直线的斜率存在时,设所求直线的方程为:y-3=k(x-1),
即kx-y+3-k=0
由点到直线的距离公式,得$\frac{|3-k|}{\sqrt{{k}^{2}+1}}$=$\sqrt{10}$,
解得k=-$\frac{1}{3}$,直线方程为:3y+x-10=0.
当直线的斜率不存在时,直线的方程为x=1不符合题意,
故所求直线的方程为:3y+x-10=0.
∴满足条件的直线有1条.
故选:B.
点评 本题考查满足条件的直线条数的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
| A. | f'(1) | B. | 3f'(1) | C. | $\frac{1}{3}f'(1)$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 30 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
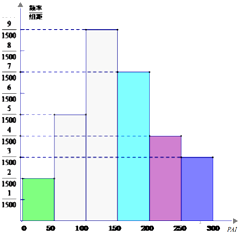 根据空气质量指数API(为整数)的不同,可将空气质量分级如表:
根据空气质量指数API(为整数)的不同,可将空气质量分级如表:| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知f(x)为定义在R上的奇函数,且当x>0时,f(x)=x2-4.
已知f(x)为定义在R上的奇函数,且当x>0时,f(x)=x2-4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一个四棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是$\frac{\sqrt{3}}{6}$,该四棱锥的最长棱的棱长为$\sqrt{2}$.
一个四棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是$\frac{\sqrt{3}}{6}$,该四棱锥的最长棱的棱长为$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com