
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
分析 分别取BB1、AB、AD、DD1中点G、H、M、N,连结FG、GH、MH、MN、EN,推导出平面EFGHMN∥平面AB1D1,由此能求出平面α截正方体的表面所得平面图形为六边形.
解答 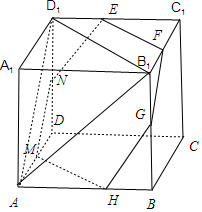 解:分别取BB1、AB、AD、DD1中点G、H、M、N,
解:分别取BB1、AB、AD、DD1中点G、H、M、N,
连结FG、GH、MH、MN、EN,
∵点E,F分别是棱D1C1,B1C1的中点,
∴EF∥MH∥B1D1,MN∥FG∥AD1,GH∥EN∥AB1,
∵MH∩GH=H,AB1∩B1D1=B1,
∴平面EFGHMN∥平面AB1D1,
∵过E,F作一平面α,使得平面α∥平面AB1D1,
∴平面α截正方体的表面所得平面图形为六边形.
故选:D.
点评 本题考查平面截正方体的表面所得平面图形判断,考查空间中线线、线面、面面间的位置关系的合理运用,考查空间想象能力,考查数形结合思想,是基础题.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
 已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x-3.
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x-3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | $({-\frac{1}{3},1}]$ | C. | [1,+∞) | D. | $({-∞,\frac{1}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
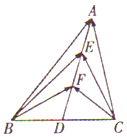 如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )| A. | 4 | B. | 8 | C. | $\frac{7}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com