
分析 (1)根据二次函数f(x)=ax2+bx+3是偶函数,且过点(2,7),可得函数解析式,进而得到F(x)的解析式,利用换元法,结合二次函数的图象和性质,可得F(x)的值域;
(2)假设对任意x∈R,都有$\frac{mx+m+4}{f(x)}<1$成立,结合二次函数的图象和性质得到矛盾,可得假设不成立.
解答 解:(1)∵二次函数f(x)=ax2+bx+3是偶函数,
∴f(-x)=f(x)恒成立,
即ax2-bx+3=ax2+bx+3恒成立,
解得:b=0,
又由函数过点(2,7),故4a+3=7m
∴a=1,
∴f(x)=x2+3,
故F(x)=22x+2x+1+7=(2x)2+2•2x+7,
令2x=t,则t>0,故F(t)=t2+2t+7=(t+1)2+6,
当t>0时F(t)>7,
∴F(x)的值域是(7,+∞).
(2)∵f(x)=x2+3>0,
假设对任意x∈R,都有$\frac{mx+m+4}{f(x)}<1$成立,
∴mx+m+4<f(x)即x2+3>mx+m+4恒成立.
即x2-mx-m-1>0恒成立,
即△=m2+4(m+1)<0,
但与△≥0矛盾,
故假不成立.
即对任意x∈R,不都有$\frac{mx+m+4}{f(x)}<1$成立.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{11}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | [2,+∞) | C. | (-∞,2] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
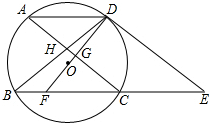 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC,BC于点G,F.
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC,BC于点G,F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
已知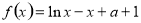 .
.
(1)若存在 使得
使得 ≥0成立,求
≥0成立,求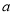 的范围;
的范围;
(2)求证:当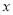 >1时,在(1)的条件下,
>1时,在(1)的条件下,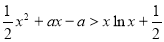 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-eln2)∪(eln2,2] | B. | [-eln2,0)∪(0,eln2] | C. | [-2,0)∪(0,2] | D. | [-e,-2)∪(2,e] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com