
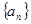 具有性质:①
具有性质:①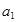 为正数;②对于任意的正整数
为正数;②对于任意的正整数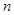 ,当
,当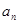 为偶数时,
为偶数时,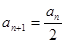 ;当
;当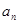 为奇数时,
为奇数时,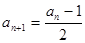
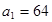 ,求数列
,求数列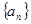 的通项公式;
的通项公式;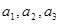 成等差数列,求
成等差数列,求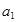 的值;
的值;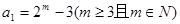 ,数列
,数列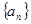 的前
的前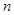 项和为
项和为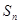 ,求证:
,求证: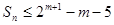
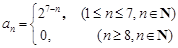 ;(2) 2;(3)证明见试题解析.
;(2) 2;(3)证明见试题解析.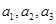
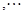 ,因为按照定义
,因为按照定义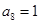 ,
,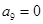 ,而此开始
,而此开始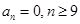 ,故可得出
,故可得出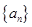 通项公式;(2)显然
通项公式;(2)显然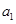 必须是整数,而且要计算
必须是整数,而且要计算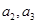 ,因此我们可以根据
,因此我们可以根据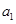 的值分类讨论(分成四类
的值分类讨论(分成四类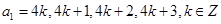 ).(3)
).(3)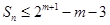 ,最好能求出
,最好能求出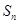 ,那么也就要求出数列
,那么也就要求出数列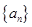 的各项,那么我们根据数列
的各项,那么我们根据数列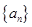 定义,由
定义,由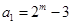 为奇数,则
为奇数,则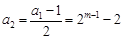 为偶数,
为偶数,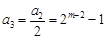 为奇数,接下来各项都是偶数,一起到某项为1,下面一项为0,以后全部为0.实际上项为1的项是第
为奇数,接下来各项都是偶数,一起到某项为1,下面一项为0,以后全部为0.实际上项为1的项是第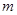 项,且
项,且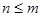 时
时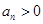 ,
,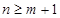 时
时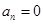 ,因此
,因此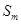 是最大的,但在计算
是最大的,但在计算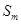 时,要注意当
时,要注意当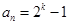 时,
时,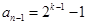 ,只要它不为0,就可继续下去.
,只要它不为0,就可继续下去.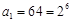 ,可得
,可得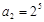 ,
,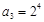 ,…,
,…,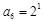 ,
,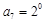 ,
,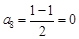 ,
,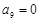 ,…,
,…,  的前7项成等比数列,从第8起数列的项均为0. (2分)
的前7项成等比数列,从第8起数列的项均为0. (2分) 的通项公式为
的通项公式为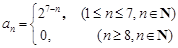 . (4分)
. (4分)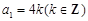 时,
时,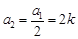 ,
,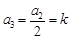 ,
,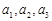 成等差数列,可知即
成等差数列,可知即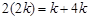 ,解得
,解得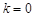 ,故
,故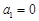 ;(舍去)
;(舍去) 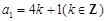 时,
时,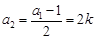 ,
,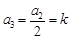 ,
,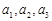 成等差数列,可知
成等差数列,可知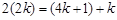 ,解得
,解得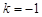 ,故
,故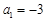 ;(舍去)(3分)
;(舍去)(3分)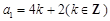 时,
时,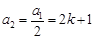 ,
,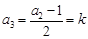 ,
,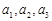 成等差数列,可知
成等差数列,可知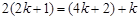 ,解得
,解得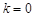 ,故
,故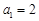 ;
;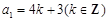 时,
时,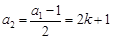 ,
,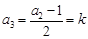 ,
,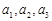 成等差数列,可知
成等差数列,可知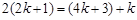 ,解得
,解得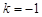 ,故
,故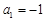 ;(舍去)
;(舍去)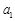 的值为2. (6分)
的值为2. (6分) (
(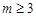 ),可得
),可得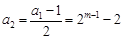 ,
,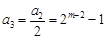 ,
,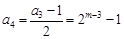 ,
,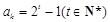 ,则
,则 是奇数,从而
是奇数,从而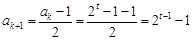 ,
,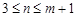 时,
时,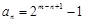 成立. (3分)
成立. (3分)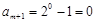 ,
,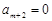 ,…
,…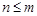 时,
时,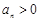 ;当
;当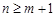 时,
时,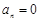 . (5分)
. (5分)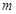 ,
,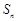 的最大值为
的最大值为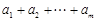
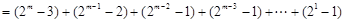
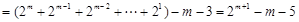 ,
,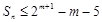 . (8分)
. (8分) 项和与最大值.
项和与最大值.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
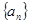 中,
中,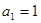 ,公差
,公差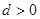 ,且它的第2项,第5项,第14项分别是等比数列
,且它的第2项,第5项,第14项分别是等比数列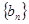 的第2项,第3项,第4项.
的第2项,第3项,第4项.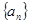 与
与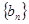 的通项公式;
的通项公式;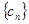 对任意自然数均有
对任意自然数均有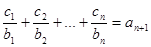 成立,求
成立,求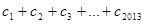 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com