
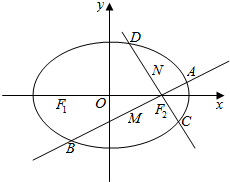
 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.分析 (Ⅰ)由已知得到关于a,b,c的方程组,求解方程组可得a,b,进而得到椭圆方程;
(Ⅱ)设直线AB的方程为x=my+1,m≠0,则直线CD的方程为x=-$\frac{1}{m}$y+1,分别代入椭圆方程,由于韦达定理和中点坐标公式可得中点M,N的坐标,求得斜率和直线方程,即可得到定点H,则△MNF2面积为S=$\frac{1}{2}$|F2H|•|yM-yN|,化简整理,再令m+$\frac{1}{m}$=t(t≥2),由于函数的单调性,即可得到最大值.
解答 解:(Ⅰ)∵椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)经过点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$),
且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,
∴$\left\{\begin{array}{l}{b=c}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{2{a}^{2}}+\frac{3}{4{b}^{2}}=1}\end{array}\right.$,解得a2=2,b2=1,
∴椭圆方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(Ⅱ)设直线AB的方程为x=my+1,m≠0,
则直线CD的方程为x=-$\frac{1}{m}$y+1,
联立$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,消去x得(m2+2)y2+2my-1=0,
设A(x1,y1),B(x2,y2),则y1+y2=-$\frac{2m}{{m}^{2}+2}$,y1y2=$\frac{-1}{{m}^{2}+2}$,
∴x1+x2=(my1+1)+(my2+1)
=m(y1+y2)+2=$\frac{4}{{m}^{2}+2}$,
由中点坐标公式得M($\frac{2}{{m}^{2}+2},-\frac{m}{{m}^{2}+2}$),
将M的坐标中的m用-$\frac{1}{m}$代换,得CD的中点N($\frac{2{m}^{2}}{2{m}^{2}+1},\frac{m}{2{m}^{2}+1}$),
kMN=$\frac{3m}{2({m}^{2}-1)}$,
直线MN的方程为y+$\frac{m}{{m}^{2}+2}$=$\frac{3m}{2({m}^{2}-1)}$(x-$\frac{2}{{m}^{2}+2}$),
即为y=$\frac{m}{{m}^{2}-1}(\frac{3}{2}x-1)$,
令$\frac{3}{2}x-1=0$,可得x=$\frac{2}{3}$,即有y=0,
则直线MN过定点H,且为H($\frac{2}{3}$,0),
∴△F2MN面积为S=$\frac{1}{2}$|F2H|•|yM-yN|
=$\frac{1}{2}$(1-$\frac{2}{3}$)•|$-\frac{m}{{m}^{2}+2}-\frac{m}{2{m}^{2}+1}$|=$\frac{1}{2}$|$\frac{{m}^{3}+m}{2{m}^{4}+5{m}^{2}+2}$|=$\frac{1}{2}$|$\frac{m+\frac{1}{m}}{2({m}^{2}+\frac{1}{{m}^{2}})+5}$|,
令m+$\frac{1}{m}$=t(t≥2),由于2t+$\frac{1}{t}$的导数为2-$\frac{1}{{t}^{2}}$,且大于0,即有在[2,+∞)递增.
即有S=$\frac{1}{2}$$•\frac{t}{2{t}^{2}+1}$=$\frac{1}{2}•\frac{1}{2t+\frac{1}{t}}$在[2,+∞)递减,
∴当t=2,即m=1时,S取得最大值,为$\frac{1}{9}$;
则△MNF2面积的最大值为$\frac{1}{9}$.
点评 本题考查椭圆方程的求法,考查直线过定点的证明,解题时要认真审题,注意直线方程、韦达定理和基本不等式和函数的单调性等知识点的合理运用,是压轴题.


科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
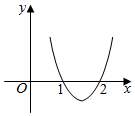 已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导导数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求x0的值和函数(x)的极小值.
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导导数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求x0的值和函数(x)的极小值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com