
分析 本题可利用分析法将原式逐步转化为容易证明的不等式,再加以证明.
解答 解:证明:因为$\sqrt{6}+\sqrt{7}$和$2\sqrt{2}+\sqrt{5}$都是整数,所以为了证明$\sqrt{6}+\sqrt{7}>2\sqrt{2}+\sqrt{5}$,
只需证${(\sqrt{6}+\sqrt{7})^2}>{(2\sqrt{2}+\sqrt{5})^2}$,
只需证$13+2\sqrt{42}>13+4\sqrt{10}$,
即证$2\sqrt{42}>4\sqrt{10}$,
即证$\sqrt{42}>2\sqrt{10}$,
即证${(\sqrt{42})^2}>{(2\sqrt{10})^2}$,
即证42>40,
因为42>40显然成立,所以原不等式成立.
点评 本题考查的是不等式证明,利用分析法很容易证明.注意分析的过程中,要求逻辑上每一步都可以逆推.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{1}{2}$<2 | B. | 1+$\frac{1}{2}$+$\frac{1}{3}$<3 | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$<3 | D. | 1+$\frac{1}{2}$+$\frac{1}{3}$<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 观察图中各正方形图案,每条边上有an个圆点,第an个图案中圆点的个数是an,按此规律推断出所有圆点总和Sn与n的关系式为( )
观察图中各正方形图案,每条边上有an个圆点,第an个图案中圆点的个数是an,按此规律推断出所有圆点总和Sn与n的关系式为( )| A. | ${S_n}=2{n^2}-2n$ | B. | ${S_n}=2{n^2}$ | C. | ${S_n}=4{n^2}-3n$ | D. | ${S_n}=2{n^2}+2n$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
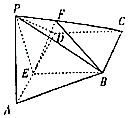 如图,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,AD∥BC,AD⊥DC,AD=DC=3,BC=2,$PD=\sqrt{2}PA=\sqrt{6}$,点F在棱PG上,且FC=2FP,点E在棱AD上,且PA∥平面BEF.
如图,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,AD∥BC,AD⊥DC,AD=DC=3,BC=2,$PD=\sqrt{2}PA=\sqrt{6}$,点F在棱PG上,且FC=2FP,点E在棱AD上,且PA∥平面BEF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com