
分析 (1)根据平面向量的坐标运算与数量积运算,求出$\overrightarrow{c}$的坐标表示,再求|$\overrightarrow{c}$|;
(2)解法一:设$\overrightarrow{c}$与$\overrightarrow{a}$的夹角为θ,根据夹角θ最小时θ=0,求出λ的值,并得出$\overrightarrow{c}$与$\overrightarrow{a}$共线同向.
解法二:设$\overrightarrow{c}$与$\overrightarrow{a}$的夹角为θ,求出夹角的表达式,利用夹角最小求出θ的值,得出λ,从而得出$\overrightarrow{c}$与$\overrightarrow{a}$共线同向.
解答 解:(1)∵$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-3,4),
∴$\overrightarrow{c}$=$\overrightarrow{a}$+λ$\overrightarrow{b}$=(1-3λ,2+4λ);
又$\overrightarrow{b}$⊥$\overrightarrow{c}$,
∴$\overrightarrow{b}$•$\overrightarrow{c}$=-3(1-3λ)+4(2+4λ)=5+25λ=0,
解得λ=-$\frac{1}{5}$,
∴$\overrightarrow{c}$=($\frac{8}{5}$,$\frac{6}{5}$),
∴|$\overrightarrow{c}$|=$\sqrt{{(\frac{8}{5})}^{2}{+(\frac{6}{5})}^{2}}$=2;
(2)解法一:设$\overrightarrow{c}$与$\overrightarrow{a}$的夹角为θ,θ∈[0,π],
要使夹角θ最小,则θ=0,即$\overrightarrow{c}$与$\overrightarrow{a}$共线同向;
∵$\overrightarrow{c}$=(1-3λ,2+4λ),$\overrightarrow{a}$=(1,2),且$\overrightarrow{c}$∥$\overrightarrow{a}$,
∴2(1-3λ)=2+4λ,解得λ=0,
此时$\overrightarrow{c}$=(1,2),满足$\overrightarrow{c}$与$\overrightarrow{a}$共线同向.
解法二:设$\overrightarrow{c}$与$\overrightarrow{a}$的夹角为θ,则
cosθ=$\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}|×|\overrightarrow{c}|}$=$\frac{5+5λ}{\sqrt{5}×\sqrt{2{5λ}^{2}+10λ+5}}$=$\frac{1+λ}{\sqrt{{5λ}^{2}+2λ+1}}$,
要$\overrightarrow{c}$与$\overrightarrow{a}$的夹角最小,则cosθ最大,
∵0≤θ≤π,故cosθ的最大值为1,此时θ=0,cosθ=1,
∴$\frac{1+λ}{\sqrt{{5λ}^{2}+2λ+1}}$=1,
解得λ=0,
∴$\overrightarrow{c}$=(1,2);
∴λ=0时,$\overrightarrow{c}$与$\overrightarrow{a}$的夹角最小,此时$\overrightarrow{c}$与$\overrightarrow{a}$共线同向.
点评 本题考查了平面向量的数量积与坐标运算的应用问题,是基础题目.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
 祖冲之之子祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行相距为h(0<h<2)的平面截该几何体,则截面面积为( )
祖冲之之子祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行相距为h(0<h<2)的平面截该几何体,则截面面积为( )| A. | 4π | B. | πh2 | C. | π(2-h)2 | D. | π(4-h2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )
某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )| A. | 2π | B. | $\sqrt{6}π$ | C. | 6π | D. | $4\sqrt{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
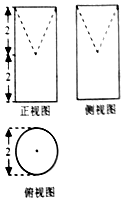
| A. | (9+$\sqrt{5}$)π | B. | (9+2$\sqrt{5}$)π | C. | (10+$\sqrt{5}$)π | D. | (10+2$\sqrt{5}$)π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | 1 | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f($\frac{π}{4}$)=-1 | B. | f(x)的周期为$\frac{π}{2}$ | C. | ω的最大值为4 | D. | f($\frac{3π}{4}$)=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com