cos+sin的值是0．题目和参考答案——青夏教育精英家教网—

8．cos（-$\frac{17}{4}$π）+sin（-$\frac{17}{4}$π）的值是0．

分析由条件利用诱导公式进行化简所给的式子，可得结果．

解答解：cos（-$\frac{17}{4}$π）+sin（-$\frac{17}{4}$π）=cos（-$\frac{π}{4}$）+sin（-$\frac{π}{4}$）=cos$\frac{π}{4}$-sin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$=0，
故答案为：0．

点评本题主要考查利用诱导公式进行化简求值，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

18．已知椭圆E的一个顶点为A（0，-1），焦点在x轴上，若椭圆右焦点到直线x-y+2$\sqrt{2}$=0的距离为3
（Ⅰ）求椭圆E的方程；
（Ⅱ）设直线l：y=kx+m（k≠0）与该椭圆交于不同的两点B，C，若坐标原点O到直线l的距离为$\frac{\sqrt{3}}{2}$，求△BOC面积的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

19．若x，y满足约束条件$\left\{\begin{array}{l}{x+y＞1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$，且目标函数z=ax+2y仅在点（1，0）处取得最小值，则a的取值范围是（　　）

A．

（-1，2）

B．

（-4，2）

C．

（-4，0）

D．

（-4，2）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

16．已知$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，4），$\overrightarrow{c}$=$\overrightarrow{a}$+λ$\overrightarrow{b}$（λ∈R）．
（1）若$\overrightarrow{b}$⊥$\overrightarrow{c}$，求|$\overrightarrow{c}$|的值；
（2）λ何值时，$\overrightarrow{c}$与$\overrightarrow{a}$的夹角最小？此时$\overrightarrow{c}$与$\overrightarrow{a}$的位置关系如何？

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．已知函数$f（x）=Asin（ωx+ϕ）（A，ω＞0，|ϕ|＜\frac{π}{2}）$的图象在y轴右侧的第一个最高点为$P（\frac{1}{3}，2）$，在y轴右侧与x轴的第一个交点为$R（\frac{5}{6}，0）$．求函数f（x）的解析式．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

13．

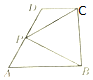如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=a（a＞0），P为线段AD（含端点）上一个动点，设$\overrightarrow{AP}=x\overrightarrow{AD}，\overrightarrow{PB}•\overrightarrow{PC}=y$，对于函数y=f（x），给出以下三个结论：①当a=2时，函数f（x）的值域为[1，4]；②对于任意的a＞0，均有f（1）=1；③对于任意的a＞0，函数f（x）的最大值均为4．其中所有正确的结论序号为②③．