
 ��ͼ����ֱ������ABCD�У�AB��CD��AB��BC��AB=2��CD=1��BC=a��a��0����PΪ�߶�AD�����˵㣩��һ�����㣬��$\overrightarrow{AP}=x\overrightarrow{AD}��\overrightarrow{PB}•\overrightarrow{PC}=y$�����ں���y=f��x�������������������ۣ��ٵ�a=2ʱ������f��x����ֵ��Ϊ[1��4]���ڶ��������a��0������f��1��=1���۶��������a��0������f��x�������ֵ��Ϊ4������������ȷ�Ľ������Ϊ�ڢۣ�
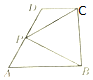
��ͼ����ֱ������ABCD�У�AB��CD��AB��BC��AB=2��CD=1��BC=a��a��0����PΪ�߶�AD�����˵㣩��һ�����㣬��$\overrightarrow{AP}=x\overrightarrow{AD}��\overrightarrow{PB}•\overrightarrow{PC}=y$�����ں���y=f��x�������������������ۣ��ٵ�a=2ʱ������f��x����ֵ��Ϊ[1��4]���ڶ��������a��0������f��1��=1���۶��������a��0������f��x�������ֵ��Ϊ4������������ȷ�Ľ������Ϊ�ڢۣ� ���� ͨ��������ͼ��ʾ������ϵ���ɵ�y=f��x��=$\overrightarrow{PB}•\overrightarrow{PC}$=��a2+1��x2-��4+a2��x+4��x��[0��1]��ͨ���������ۣ����ö��κ����ĵ����Լ����жϳ���
��� �⣺��ͼ��ʾ������ֱ������ϵ��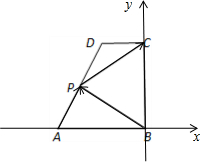 ����ֱ������ABCD�У�AB��CD��AB��BC��AB=2��CD=1��BC=a��a��0����
����ֱ������ABCD�У�AB��CD��AB��BC��AB=2��CD=1��BC=a��a��0����
��B��0��0����A��-2��0����D��-1��a����C��0��a����
��$\overrightarrow{AP}=x\overrightarrow{AD}$����0��x��1������$\overrightarrow{BP}=\overrightarrow{BA}+x\overrightarrow{AD}$=��-2��0��+x��1��a��=��x-2��xa����
$\overrightarrow{PC}=\overrightarrow{BC}-\overrightarrow{BP}$=��0��a��-��x-2��xa��=��2-x��a-xa����
��y=f��x��=$\overrightarrow{PB}•\overrightarrow{PC}$=��a2+1��x2-��4+a2��x+4��x��[0��1]��
�ٵ�a=2ʱ��y=f��x��=5x2-8x+4=5��x-$\frac{4}{5}$��+$\frac{4}{5}$��
��0��x��1���൱x=$\frac{4}{5}$ʱ��f��x��ȡ����Сֵ$\frac{4}{5}$��
��f��0��=4��f��1��=1����f��x��max=f��0��=4��
���Ͽɵã�����f��x����ֵ��Ϊ[$\frac{4}{5}$��4]��
��ˢٲ���ȷ��
����y=f��x��=��a2+1��x2-��4+a2��x+4��
�ɵã�?a�ʣ�0��+�ޣ�������f��1��=1��������ˢ���ȷ��
����y=f��x��=��a2+1��x2-��4+a2��x+4��
��֪���Գ���x0=$\frac{4+{a}^{2}}{2{a}^{2}+2}$��
��0��a��$\sqrt{2}$ʱ��1��x0���ຯ��f��x����[0��1]�����ݼ�����˵�x=0ʱ������f��x��ȡ�����ֵ4��
��a$��\sqrt{2}$ʱ��0��x0��1������f��x����[0��x0�������ݼ����ڣ�x0��1]�ϵ���������
��f��0��=4��f��1��=1����f��x��max=f��0��=4����ˢ���ȷ��
���Ͽ�֪��ֻ�Тڢ���ȷ��
�ʴ�Ϊ���ڢۣ�
���� ���⿼�������������㡢�������ۡ����κ����ĵ����ԵȻ���֪ʶ��������ܷ��������������������ͼ����������������⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
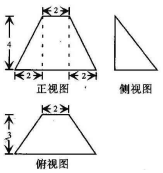
| A�� | 16 | B�� | 20 | C�� | 52 | D�� | 60 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
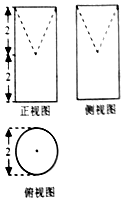
| A�� | ��9+$\sqrt{5}$���� | B�� | ��9+2$\sqrt{5}$���� | C�� | ��10+$\sqrt{5}$���� | D�� | ��10+2$\sqrt{5}$���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������һ��$\frac{1}{2��k+1��}$ | |
| B�� | ����������$\frac{1}{2k+1}+\frac{1}{2��k+1��}$ | |
| C�� | ������һ��$\frac{1}{2��k+1��}$���ּ�����һ��$\frac{1}{k+1}$ | |
| D�� | ����������$\frac{1}{2k+1}+\frac{1}{2��k+1��}$���ּ�����һ��$\frac{1}{k+1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{5}}}{5}$ | B�� | 1 | C�� | $\sqrt{5}$ | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ������x | 2 | 3 | 5 | 6 |
| ���۶�y | 7 | m | 9 | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com