
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| �� |
| 6 |
| �� |
| 4 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| �� |
| 6 |
| �� |
| 4 |
| �� |
| 6 |
| �� |
| 6 |
| 7�� |
| 6 |
| �� |
| 6 |
| �� |
| 4 |
| A+B |
| 2 |
| A-B |
| 2 |
| 15��+75�� |
| 2 |
| 15��-75�� |
| 2 |
| ||
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| �� |
| 6 |
| 1 |
| 2 |
| �� |
| 6 |
| �� |
| 6 |
| 1 |
| 2 |
| �� |
| 6 |
| ||
| 4 |
| �� |
| 4 |
| �� |
| 6 |
| �� |
| 6 |
| 7�� |
| 6 |
| ||
| 2 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 5 |
| 4 |
| �� |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
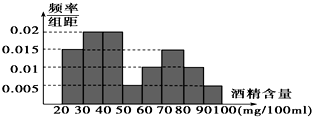 �ݡ�����������������2013��8��1����8��28�գ�ij�н��ܲ��Ź������1000����������ƺ�ݳ������Ƽݳ��ļ�ʻԱ80�ˣ�ͼʾ�Ƕ���80��ѪҺ�оƾ��������м�����ý����Ƶ�ʷֲ�ֱ��ͼ��
�ݡ�����������������2013��8��1����8��28�գ�ij�н��ܲ��Ź������1000����������ƺ�ݳ������Ƽݳ��ļ�ʻԱ80�ˣ�ͼʾ�Ƕ���80��ѪҺ�оƾ��������м�����ý����Ƶ�ʷֲ�ֱ��ͼ��| �ƾ���������λ��mg/100ml�� | [20��30�� | [30��40�� | [40��50�� | [50��60�� |
| ���� | ||||
| �ƾ���������λ��mg/100ml�� | [60��70�� | [70��80�� | [80��90�� | [90��100] |
| ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ��עNBA | ����עNBA | �ϼ� | |
| ���� | 6 | ||
| �� | 10 | ||
| �ϼ� | 48 |
| 2 |
| 3 |
| P��K2��k�� | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ����ͼ��ʾ�ļ������У��ı���ABCDΪ�����Σ���ABEΪ����ֱ�������Σ���BAE=90�㣬��AD��AE��
����ͼ��ʾ�ļ������У��ı���ABCDΪ�����Σ���ABEΪ����ֱ�������Σ���BAE=90�㣬��AD��AE���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com