
 在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和A1B1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和A1B1的中点.分析 以D为坐标原点,以DA,DC,DD1分别为x轴、y轴、z轴正方向建立空间直角坐标系.求出B,C1,E,F的坐标,
(Ⅰ)求出面FC1B1的一个法向,面BFC1的法向量,利用空间向量的数量积求解二面角B-FC1-B1的余弦值.
(Ⅱ)设P(x,y,0)(0≤x≤1,0≤y≤1),利用EP∥平面BFC1,推出$\overrightarrow{EP}⊥\overrightarrow{n_2}$,求出x,y的关系,利用空间距离结合二次函数的最值求解即可.
解答 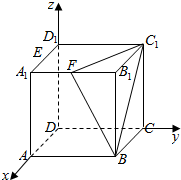 解:以D为坐标原点,以DA,DC,DD1分别为x轴、y轴、z轴正方向建立空间直角坐标系.
解:以D为坐标原点,以DA,DC,DD1分别为x轴、y轴、z轴正方向建立空间直角坐标系.
则$B(1,1,0),{C_1}(0,1,1),E(\frac{1}{2},0,1),F(1,\frac{1}{2},1)$.
(Ⅰ)由图可取面FC1B1的一个法向量$\overrightarrow{n_1}=({0,0,1})$;$\overrightarrow{B{C_1}}=({-1,0,1}),\overrightarrow{BF}=({0,-\frac{1}{2},1})$,设面BFC1的法向量为$\overrightarrow{n_2}$,则$\left\{{\begin{array}{l}{\overrightarrow{n_2}•\overrightarrow{B{C_1}}=0}\\{\overrightarrow{n_2}•\overrightarrow{BF}=0}\end{array}}\right.$,可取$\overrightarrow{n_2}=({1,2,1})$.
所以$cos\left?{\overrightarrow{n_1},\overrightarrow{n_2}}\right>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|{\overrightarrow{n_1}}||{\overrightarrow{n_2}}|}}=\frac{{\sqrt{6}}}{6}$,
即二面角B-FC1-B1的余弦值为$\frac{{\sqrt{6}}}{6}$.
(Ⅱ)因为P在正方形ABCD内部及边界上,所以可设P(x,y,0)(0≤x≤1,0≤y≤1),
则$\overrightarrow{EP}=({x-\frac{1}{2},y,-1})$.
因为EP∥平面BFC1,所以$\overrightarrow{EP}⊥\overrightarrow{n_2}$,即$({x-\frac{1}{2},y,-1})•$(1,2,1)=0,
所以$x=-2y+\frac{3}{2}$,∵0≤x≤1,0≤y≤1,
∴$0≤-2y+\frac{3}{2}≤1,0≤y≤1$,∴$\frac{1}{4}≤y≤\frac{3}{4}$,
所以$|{\overrightarrow{EP}}|=\sqrt{{{({x-\frac{1}{2}})}^2}+{y^2}+1}$=$\sqrt{{{({2y-1})}^2}+{y^2}+1}=\sqrt{5{y^2}-4y+2}=\sqrt{5{{({y-\frac{2}{5}})}^2}+\frac{6}{5}}$,
当$y=\frac{2}{5}$时,${|{\overrightarrow{EP}}|_{min}}=\frac{{\sqrt{30}}}{5}$.
点评 本题看v我没觉得平面角的求法,空间距离公式的应用,考查转化思想以及计算能力.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
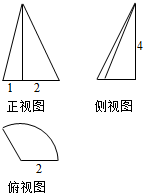
| A. | $\frac{2π}{3}$ | B. | $\frac{16π}{9}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
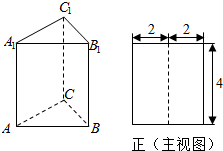 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为4,且侧棱AA1⊥底面ABC,其正(主)视图是边长为4的正方形,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为4,且侧棱AA1⊥底面ABC,其正(主)视图是边长为4的正方形,则此三棱柱侧(左)视图的面积为( )| A. | 16 | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com