
分析 化简$\frac{1+i}{1-i}$=$\frac{(1+i)^{2}}{(1-i)(1+i)}$=i,$\frac{1-i}{1+i}$=-i,代入即可得出.
解答 解:∵$\frac{1+i}{1-i}$=$\frac{(1+i)^{2}}{(1-i)(1+i)}$=$\frac{2i}{2}$=i,∴$\frac{1-i}{1+i}$=$\frac{1}{i}=-i$,
∴f(n)=${(\frac{1+i}{1-i})^{2n}}$+${(\frac{1-i}{1+i})^{2n}}$=i2n+(-i)2n=2(-1)n=±2,
∴集合{f(n)}={-2,2}.
故答案为:{-2,2}.
点评 本题考查了复数的运算法则,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
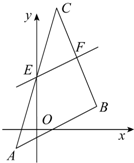 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的$\frac{1}{4}$.求:
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的$\frac{1}{4}$.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | $\sqrt{13}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,an=($\frac{1}{3}$)n,把数列{an}的各项排成如下三角形:记A(s,t)表示第s行第t个数,则A(6,2)=($\frac{1}{3}$)38.
如图所示,an=($\frac{1}{3}$)n,把数列{an}的各项排成如下三角形:记A(s,t)表示第s行第t个数,则A(6,2)=($\frac{1}{3}$)38.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com