Question

15．在矩形ABCD中，对角线AC与相邻两边所成的角分别为α、β，则有sin²α+sin²β=1，类比到空间中的一个正确命题是：在长方体ABCD-A₁B₁C₁D₁中，对角线AC₁与相邻三个面所成的角分别为α、β、γ，则sin²α+sin²β+sin²γ=1．

Answer 1

分析 由在长方形中，设一条对角线与其一顶点出发的两条边所成的角分别是α，β，则有sin²α+sin²β=1，我们根据平面性质可以类比推断出空间性质，我们易得答案．

解答 解：有如下命题：长方体ABCD-A₁B₁C₁D₁中，对角线A₁C与平面A₁B、A₁C₁、A₁D所成的角分别为α、β、γ，则 sin²α+sin²β+sin²γ=1．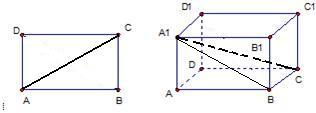
证明：如图，对角线A₁C与平面A₁B所成的角为∠CA₁B=α，
在直角三角形CA₁B中，sin²α=$\frac{B{C}^{2}}{{A}_{1}{C}^{2}}$，
同理：sin²β=$\frac{C{{C}_{1}}^{2}}{{A}_{1}{C}^{2}}$，sin²γ=$\frac{C{D}^{2}}{{C}_{1}{C}^{2}}$
∴sin²α+sin²β+sin²γ=$\frac{B{C}^{2}}{{A}_{1}{C}^{2}}$+$\frac{C{{C}_{1}}^{2}}{{A}_{1}{C}^{2}}$+$\frac{C{D}^{2}}{{C}_{1}{C}^{2}}$=1．
故答案为：1．

点评 本题考查的知识点是类比推理，在由平面图形的性质向空间物体的性质进行类比时，常用的思路有：由平面图形中点的性质类比推理出空间里的线的性质，由平面图形中线的性质类比推理出空间中面的性质，由平面图形中面的性质类比推理出空间中体的性质，或是将平面中的两维性质，类比推断到空间中的三维性质．