
 如图,已知直线l过点A(0,4),交函数y=2x的图象于点C,A交x轴于点B,若$\overrightarrow{AC}$=$\frac{2}{3}$$\overrightarrow{CB}$,则点B的横坐标为3.16.(结果精确到0.01,参考数据lg2=0.3010,lg3=0.4771,)
如图,已知直线l过点A(0,4),交函数y=2x的图象于点C,A交x轴于点B,若$\overrightarrow{AC}$=$\frac{2}{3}$$\overrightarrow{CB}$,则点B的横坐标为3.16.(结果精确到0.01,参考数据lg2=0.3010,lg3=0.4771,) 分析 过C作CD∥x轴交y轴于D,作CE∥y轴交x轴于E,设B(x,0),利用相似三角形求出C点坐标,代入函数解析式计算即可.
解答 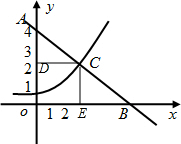 解:过C作CD∥x轴交y轴于D,作CE∥y轴交x轴于E,
解:过C作CD∥x轴交y轴于D,作CE∥y轴交x轴于E,
∴$\frac{CD}{OB}=\frac{AC}{AB}=\frac{2}{5}$,$\frac{CE}{OA}=\frac{BC}{AB}=\frac{3}{5}$,
∴CD=$\frac{2}{5}OB$.CE=$\frac{12}{5}$.
∴设B(x,0),则C($\frac{2}{5}x$,$\frac{12}{5}$).
∵C在函数y=2x的图象上,
∴$\frac{12}{5}$=2${\;}^{\frac{2x}{5}}$,
∴$\frac{2x}{5}$=log2$\frac{12}{5}$=$\frac{lg12-lg5}{lg2}$=$\frac{lg3+2lg2-(1-lg2)}{lg2}$=$\frac{lg3+3lg2-1}{lg2}$.
∴x=$\frac{5}{2}$•$\frac{lg3+3lg2-1}{lg2}$≈3.16.
故答案为:3.16.
点评 本题考查了对数的运算性质,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 90° | B. | 60° | C. | 30° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com