
 ��k��0��������y1=��x-k��2+2k��y2=-��x+k��2-2k��ͼ����y�����ν���A��B���㣬����y1��y2��ͼ��Ķ���ֱ�ΪC��D��
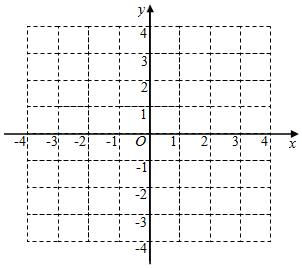
��k��0��������y1=��x-k��2+2k��y2=-��x+k��2-2k��ͼ����y�����ν���A��B���㣬����y1��y2��ͼ��Ķ���ֱ�ΪC��D������ ��1��ȡk=1�ɵ�����������ʽ����������ͼ��
��2���ɺ�������ʽ���A��B��C��D�����꣬��һ�����AB�����ö��κ�����÷�Χ��
��3���ֱ����AC��BD��AD��BC����ֱ�ߵ�б�ʣ���б����ȿɵ�A��B��C��D�ĵ㹹�ɵ��ı���ADBC��ƽ���ı��Σ����ɶԽ���б�ʷ�����֪�ı���ADBC���ܹ������Σ�
���  �⣺��1����ͼ��${y}_{1}=��x-1��^{2}+2��{y}_{2}=-��x+1��^{2}-2$��
�⣺��1����ͼ��${y}_{1}=��x-1��^{2}+2��{y}_{2}=-��x+1��^{2}-2$��
��2���ں���y1=��x-k��2+2k��y2=-��x+k��2-2k�У�
�ֱ�ȡx=0����${y}_{1}={k}^{2}+2k��{y}_{2}=-{k}^{2}-2k$��
��A��0��k2+2k����B��0��-k2-2k����
��|AB|=|k2+2k+k2+2k|=2|k2+2k|��
��-2��k��0����k2+2k��[-1��0����
��|AB|=2|k2+2k|�ʣ�0��2]��
��3��������ɵã�A��0��k2+2k����B��0��-k2-2k����
C��k��2k����D��-k��-2k����
��${k}_{AC}=\frac{{k}^{2}}{-k}=-k��{k}_{BD}=\frac{-{k}^{2}}{k}=-k$��${k}_{AD}=\frac{{k}^{2}+4k}{k}=k+4��{k}_{BC}=\frac{-{k}^{2}-4k}{-k}=k+4$��
��A��B��C��D�ĵ㹹�ɵ��ı���ADBC��ƽ���ı��Σ�
��${k}_{CD}=\frac{4k}{2k}=2$����AB��б�ʲ����ڣ�
��ܹ������Σ�
���� ���⿼�麯����ͼ�����˺�������ʽ����⼰���÷��������������ν�ϵĽ���˼�뷽�������е��⣮


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -8 | B�� | -4 | C�� | 4 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24 | B�� | 18 | C�� | 16 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12 | B�� | 24 | C�� | 36 | D�� | 120 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com