
分析 由f(f(x0))=x0得f-1(x0)=f(x0),
根据f(x)与f-1(x)的对称关系可得f(x0)=x0,
于是f(x0)∈[0,1],分离参数得到a的范围.
解答 解:∵f(f(x0))=x0,
∴f-1(x0)=f(x0),
∵f-1(x)和f(x)关于直线y=x对称,
∴f(x0)=x0,
∵x0∈[0,1],
∴0≤$\sqrt{ln{(x}_{0}+1)+{2x}_{0}-a}$≤1,
即0≤ln(x0+1)+2x0-a≤1.
∴-[ln(x0+1)+2x0]≤-a≤1-[ln(x0+1)+2x0]
∴[ln(x0+1)+2x0]-1≤a≤ln(x0+1)+2x0]
∵存在x0∈[0,1]使f(f(x0))=x0,
∴-1≤a≤2+ln2.
故答案为:[-1,2+ln2].
点评 本题考查了反函数的性质以及函数最值的应用问题,是较难的题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
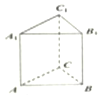 如图,在直三棱柱ABC-A1B1C1中,∠CAB=90°,AC=AB=AA1,则异面直线AC1,A1B所成角的余弦值为( )
如图,在直三棱柱ABC-A1B1C1中,∠CAB=90°,AC=AB=AA1,则异面直线AC1,A1B所成角的余弦值为( )| A. | $-\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3盏灯 | B. | 192盏灯 | C. | 195盏灯 | D. | 200盏灯 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{15}}{4}$ | B. | $\frac{\sqrt{15}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com